В статье объясняется, как работает кодировщик в нейронной сети, подробно описываются шаги, связанные с подготовкой данных и вычислением представлений токенов. Она начинается с инициализации набора данных и описывает цикл обучения, включая то, как данные группируются в пакеты (батчи) для обработки.
Обсуждаются такие ключевые процессы, как embedding, dropout, нормализация и механизм внимания, с упором на роли различных компонентов, таких как SelfAttentionEncoderLayer и LayerNorm. В статье также рассматриваются линейные преобразования и использование относительного позиционного кодирования, объясняется, как входные данные преобразуются через несколько слоев перед отправкой в декодер. В целом, данная статья обеспечивает полное понимание функциональности кодировщика и его важности в моделях машинного обучения.
Начало работы кодировщика
После инициализации выполняются следующие шаги:
- набор данных финализируется, т. е. активируется весь конвейер подготовки обучающих данных;
├── dataset = self._finalize_dataset() модуль training.py
- цикл запускается с количеством шагов, указанным в параметре Train steps ;
- на каждом шаге цикла обучения из обучающего набора данных извлекаются группы, сгруппированные в пакеты;
- количество групп будет равно эффективному размеру пакета // размер пакета. Например, если задать параметр эффективный размер пакета = 200 000, а размер пакета = 6 250, то количество групп будет равно 200 000 // 6 250 = 32.
- в каждой из 32 групп будет 6250 токенов, поэтому общий объем токенов, который будет обработан за один шаг обучения, будет равен эффективному размеру пакета или батча, т. е. 200 000 токенов.
- из группы извлекается из партий, и для каждого токена в партиях из матрицы встраивания извлекается векторное представление токена с помощью функции tf.nn.embedding_lookup.
├── call() | class WordEmbedder(TextInputter) модуль text_inputter.py
На примере нашей модели с vocab_size = 26 и num_units = 4, схематически для исходного языка это можно представить следующим образом: (Изображение 1 - матрица встраивания)
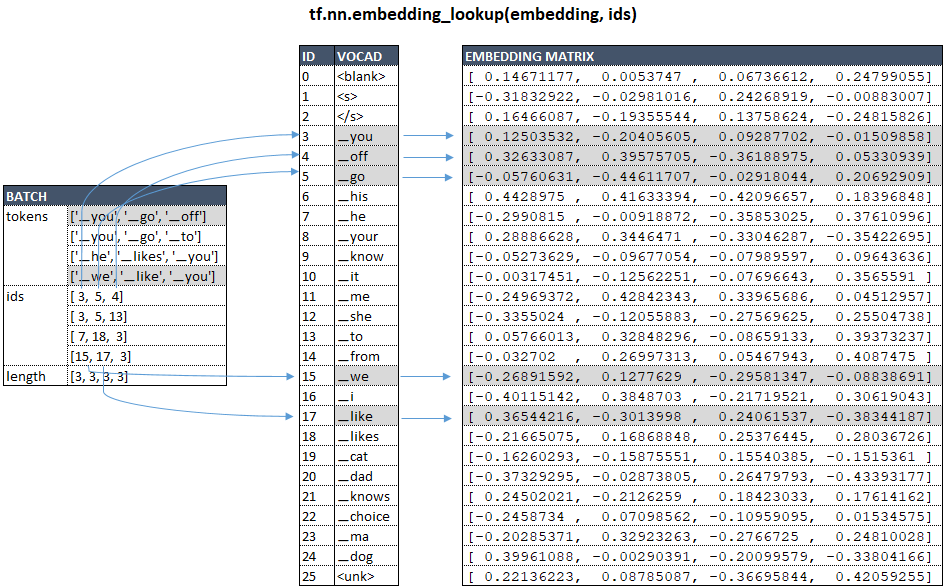
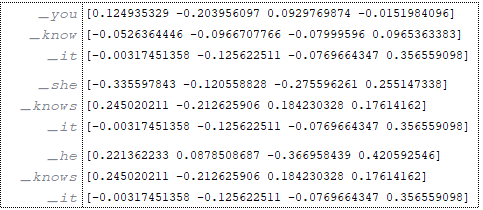
Предположим, что наши партии состоят из 3 обучающих элементов.
Источник: (Изображение 2 - источник)
Цель: (Изображение 3 - цель)
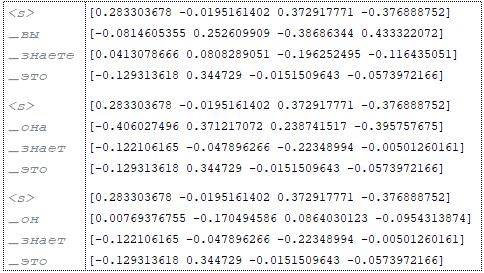
В КОДИРОВАНИИ ВЕКТОРА ПОДГОТОВКИ ТОКЕНОВ исходный ЯЗЫК:
- умножается на квадратный корень размерности - входы = входы * √numunits например num_units = 4 ; (Изображение 4 - num_units = 4)
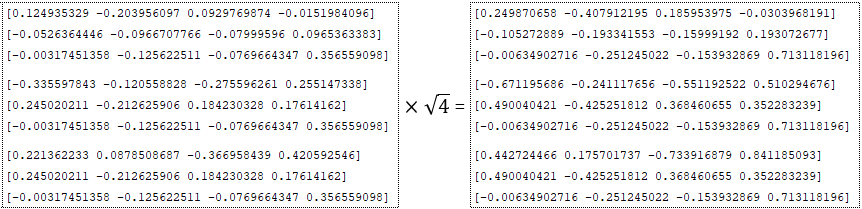
- применяется dropout (параметр dropout из файла конфигурации), т.е. значения случайным образом заменяются на ноль с помощью функции tf.nn.dropout. При этом все остальные значения (кроме замененных на ноль) корректируются путем умножения на 1/(1 - p), где p - вероятность dropout. Это делается для приведения значений к одному масштабу, что позволяет использовать одну и ту же сеть для обучения (при вероятности < 1,0) и вывода (при вероятности = 1,0); (Изображение 5 - параметр dropout)

- По размерности партий функция sequence_mask">tf.sequence_mask строит тензор маски; для нашего примера размерность партий будет [3 3 3] и функция возвращает маску; (Изображение 6 - sequence_mask">tf.sequence_mask)
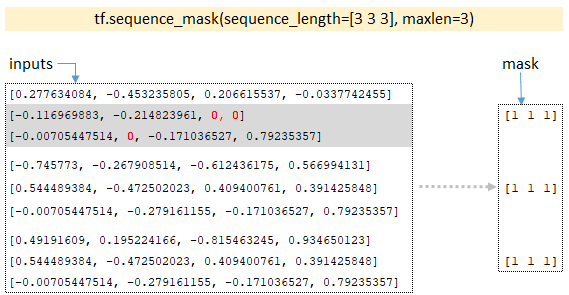
- В цикле для каждого слоя, равного числу параметров Layers, векторное представление пакетированного вектора (которое хранится в переменных inputs ) и тензор маски передаются в слой, а затем результат, возвращаемый слоем, передается в следующий слой. Например, если у нас 6 слоев, результат из первого слоя будет входным результатом для второго слоя и т. д.

- Каждый слой представляет собой объект класса SelfAttentionEncoderLayer, в котором механизм внимания реализован с помощью класса MultiHeadAttention. Механизм преобразований, происходящих в каждом слое SelfAttentionEncoderLayer, будет описан ниже.
Нормализационный слой, класс LayerNorm()
При параметре Pre norm = True к пакету после операции исключения и маскирования, перед расчетом весов внимания, применяется слой нормализации — для каждого пакета со значениями k мы вычисляем среднее значение и дисперсию:
- mean_i = sum(x_i[j] for j in range(k))/k
- var_i = sum((x_i[j] - mean_i) ** 2 for j in range(k))/k
Затем вычисляется нормализованное значение x_i_normalized, включая небольшой фактор эпсилон (0,001) для числовой устойчивости:
- x_i_normalized = (x_i — mean_i) / sqrt(var_i + epsilon)
И, наконец, x_i_normalized линейно преобразуется с использованием гаммы и беты, которые являются обучаемыми параметрами (при инициализации гамма = [1,..., 1], бета = [0,..., 0]):
- output_i = x_i_normalized * gamma + beta
Значения вычисляются матрицы запросов - нормализованные значения матрицы входов, полученные на предыдущем шаге, пропускаются через линейное преобразование слоя tf.keras.layers.Dense.
Линейное преобразование, класс Dense()
━ 1) вычисляется размерность партий → shape = [3, 3, 4] ;
━ 2) изменяет размерность tf.reshape (inputs, [-1, shape[-1]]) → tf.reshape(inputs, [-1, 4]); (Изображение 7 - tf.reshape)

━ 3) при mixed_precision и num_units, делящихся на 8, вычисляется размер отступа и его формирование
- padding_size = 8 - num_units % 8 → padding_size = 8 - 4 % 8 = 4
- paddings = [[0, 0], [0, padding_size]] → paddings = [[0, 0], [0, 4]]
веса слоя ядра (которые были сформированы при инициализации) матрицы запросов дополняются отступом tf.pad(kernel, paddings); (Изображение 8 - tf.pad)

━ 4) матрицы kernel и batched матрица (входы) tf.matmul(inputs, kernel) умножаются; (Изображение 9 - tf.matmul)

━ 5) из полученной матрицы берется срез размерности слоя num_units и формируется матрица выходов; (Изображение 10 - outputs матрица)

━ 6) вектор смещения добавляется к outputs матрице, полученной на предыдущем шаге (начальные значения смещения инициализируются слоем ядра и изначально равны нулю) tf.nn.bias_add(outputs, bias); (Изображение 11 - tf.nn.bias_add)
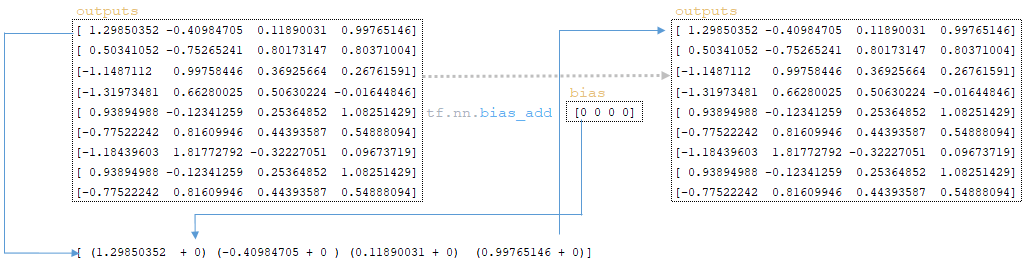
━ 7) после добавления смещения outputs матрица подвергается линейной активации слоя activation(outputs). Линейная активация слоя - это применение функции к матрице. Поскольку функция для слоя tf.keras.layers.Dense не определена, по умолчанию функция активации равна a(x) = x, т. е. матрица остается неизменной; (Изображение 12 - activation)
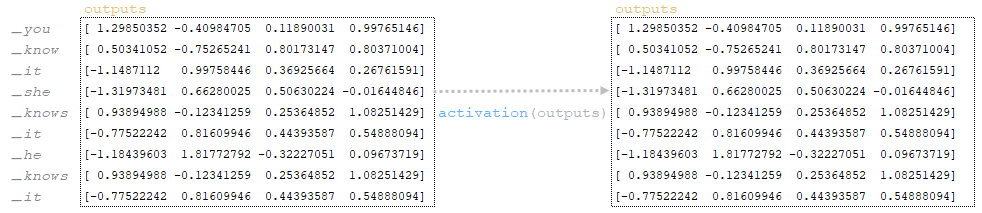
━ 8) после активации линейного слоя матрица выходов преобразуется tf.reshape(outputs, shape[:-1] + [num_units]) → tf.reshape(outputs, [3, 3, 4]). После этого шага мы получаем queries матрицу. (Изображение 13 - матрица queries)

Полученная на предыдущем шаге матрица queries делится на количество голов (в нашей архитектуре количество голов равно 2, механизм деления описан в первой части статьи). (Изображение 14 - матрица запросов делится на количество голов)
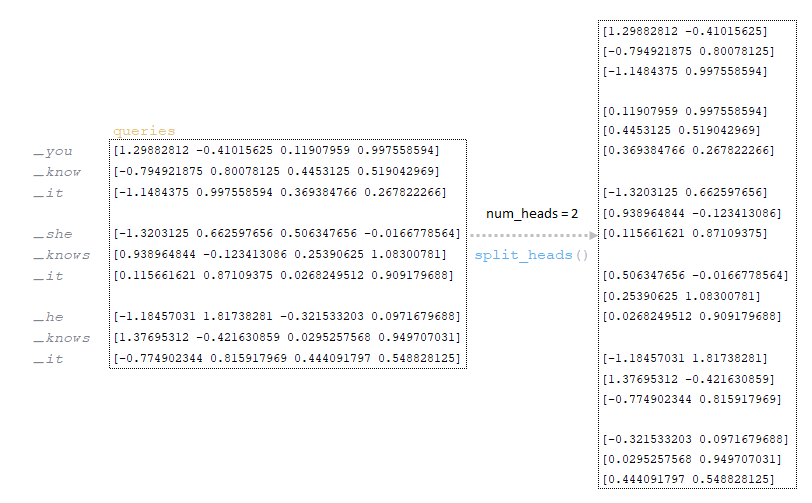
Делящаяся на количество голов матрица queries делится на квадратный корень: (Изображение 15 - матрица запросов делится на квадратный корень)

- num_units_per_head:
- num_units_per_head = num_units // num_heads
- num_units_per_head = 4 // 2 = 2
Согласно шагам 1-8, описанным выше (пункт Линейное преобразование), вычисляется матрица ключей и делится на количество целей. (Изображение 16 - keys матрица)

Следуя шагам 1-8 выше, вычисляется матрица значений и делится на количество целей. (Изображение 17 - values матрица)

Относительное кодирование
Так как в рассматриваемом примере используется относительное позиционное кодирование ( maximum_relative_position = 8 ), то следующим шагом будет относительное кодирование:
━ 1) вычисляется размерность keys матрицы:
- keys_length = tf.shape(keys)[2]
- keys_length = [3 2 3 2 2][2]
- keys_length = 3;
━ 2) формируется массив целочисленных элементов длины keys_length:
- arange = tf.range(length)
- arange = [0 1 2];
━ 3) формируются две матрицы на оси 0 и 1 с помощью функции tf.expand_dims(input, axis) и из полученных матриц вычисляется расстояние до диагонали distance = tf.expand_dims(arange, 0) - tf.expand_dims(arange, 1); (Изображение 18 - distance матрица)
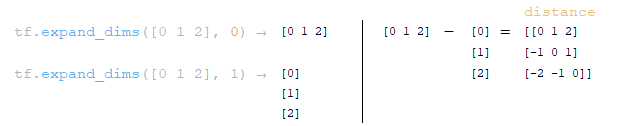
━ 4) матрица расстояний до диагонали расстояний отсекается по значению maximum_relative_position tf.clip_by_value(distance, -maximum_position, maximum_position); (Изображение 19 - maximum_relative_position)
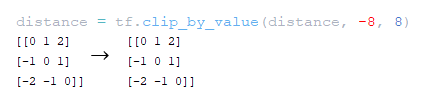
━ 5) значение maximum_relative_position добавляется к матрице расстояний, полученной на предыдущем шаге; (Изображение 20 - матрица distance + maximum_position )
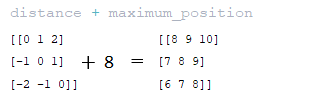
━ 6) матрица relation_pos, полученная на предыдущем шаге, используется для извлечения из матрицы relation_position_keys, сформированной при инициализации модели, соответствующих элементов по индексам с помощью функции tf.nn.embedding_lookup. Затем формируется матрица relation_repr_keys ; (Изображение 21 - матрица relation_repr_keys)
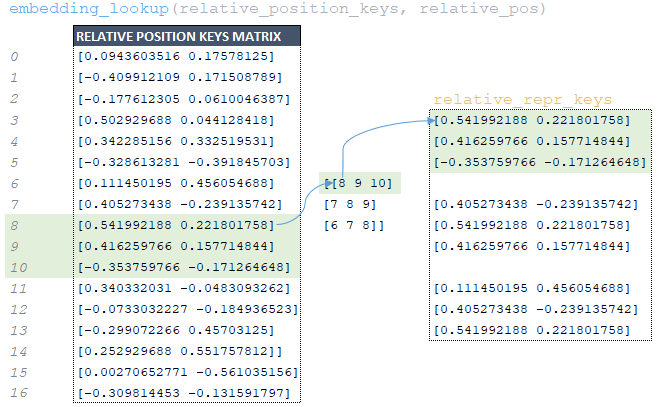
━ 7) матрица relation_repr_values → embedding_lookup (relative_position_values, relation_pos) формируется таким же образом; (Изображение 22 - матрица relation_repr_values)
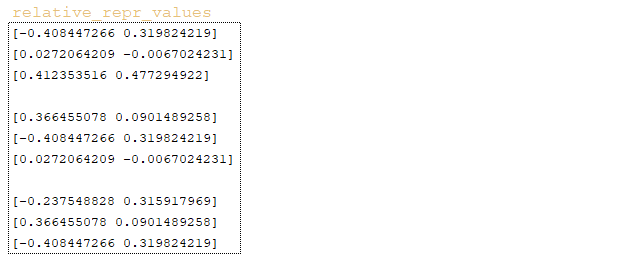
Скалярное произведение
Следующий шаг — скалярное произведение queries и keys матриц → dot = tf.matmul(queries, keys, transpose_b =True). (Изображение 23 — скалярное произведение матриц запросов и ключей)
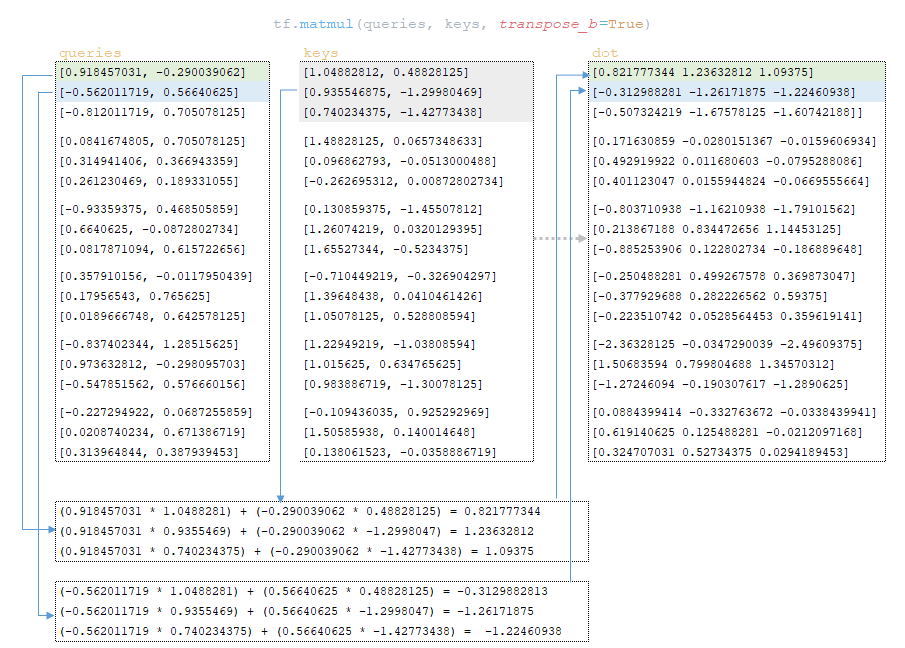
Матрица queries умножается на матрицу relation_repr_keys → matmul_with_relative_representations (queries, relation_repr_keys, transpose_b =True). (Изображение 24 — матрица запросов умножается на матрицу relation_repr_keys)
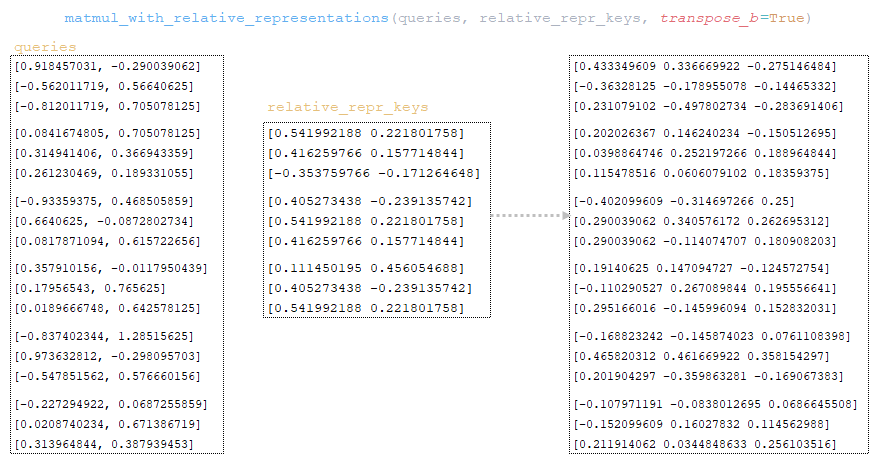
К dot матрице добавляется матрица, полученная на шаге matmul_with_relative_representations. (Изображение 25 — точечная матрица)

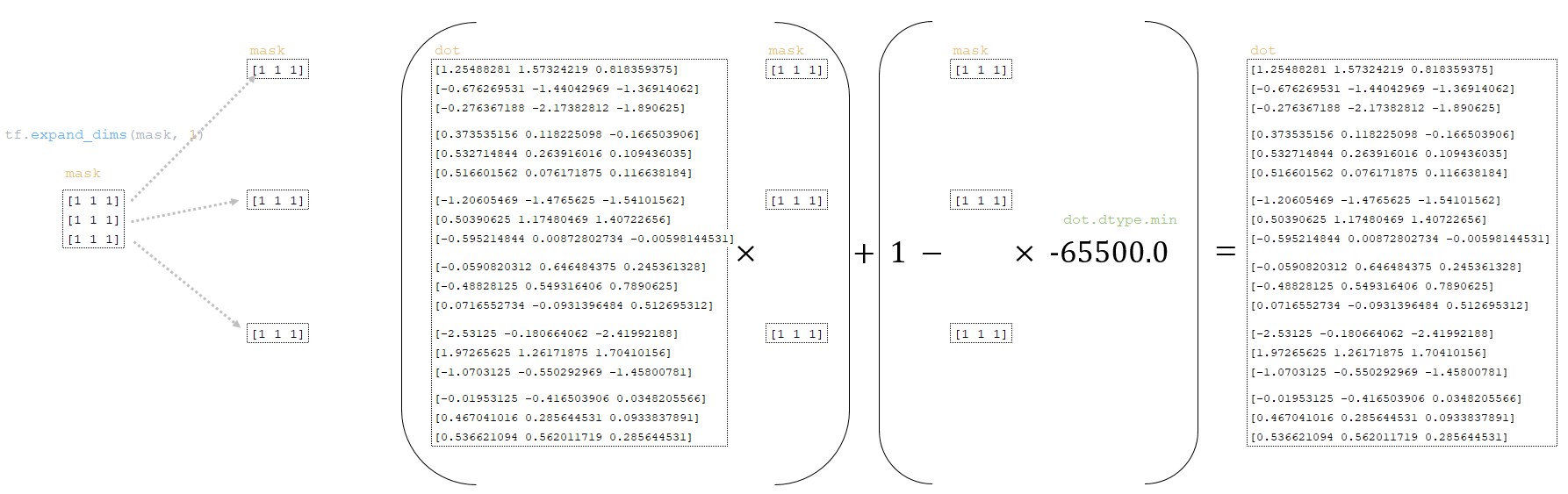
Dot матрица преобразуется с использованием mask матрицы, полученной из партий токенов выше:
━ 1) размерность mask матрицы изменяется
mask = tf.expand_dims(mask, 1)
━ 2) dot матрица преобразуется следующим образом
dot = (dot * mask) + (1.0 - mask) * dot.dtype.min
(Изображение 26 - матрицы точек и масок)
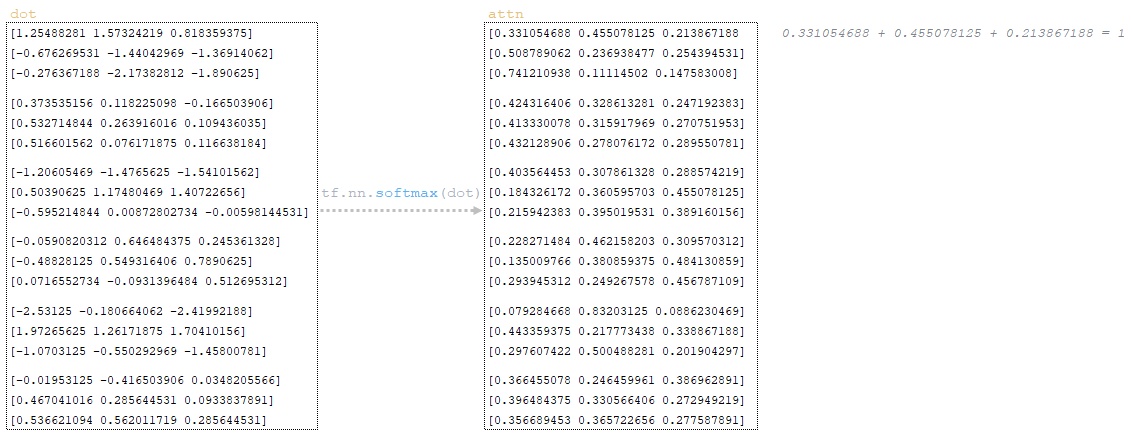
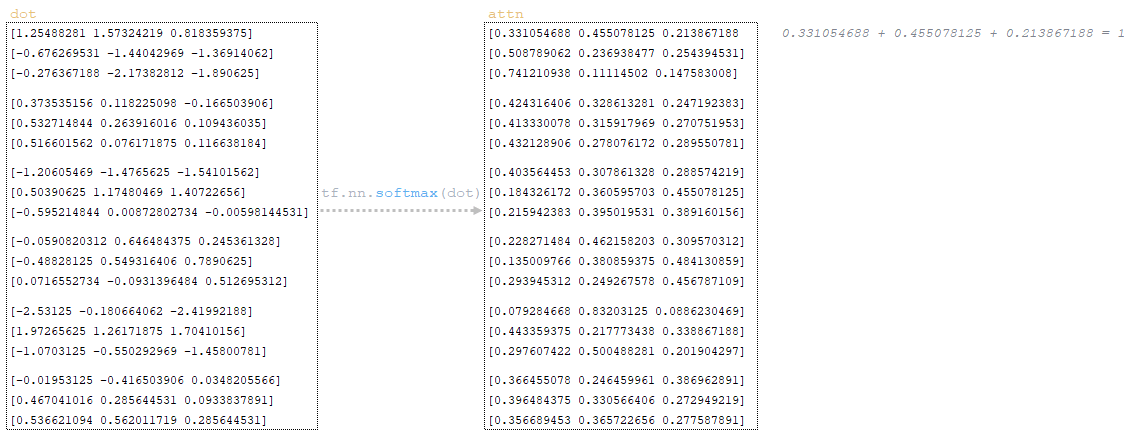
Функция активации softmax применяется к dot матрице, и мы получаем матрицу attn → attn = tf.nn.softmax(dot). Функция softmax используется для преобразования вектора значений в распределение вероятностей, сумма которых равна 1. (Изображение 27 - применение softmax)
Dropout применяется к матрице attn (параметр awareness_dropout из файла конфигурации). (Изображение 28 - применение dropout)
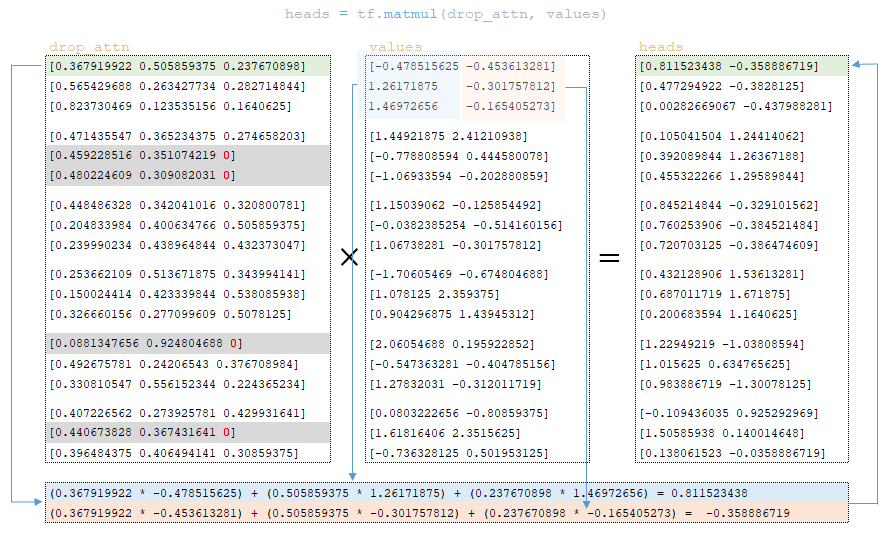
После dropout матрица drop_attn умножается на матрицу values для формирования матрицы heads. (Изображение 29 - матрица heads)
Матрица drop_attn умножается на матрицу relation_repr_values. (Изображение 30 - матрица drop_attn )
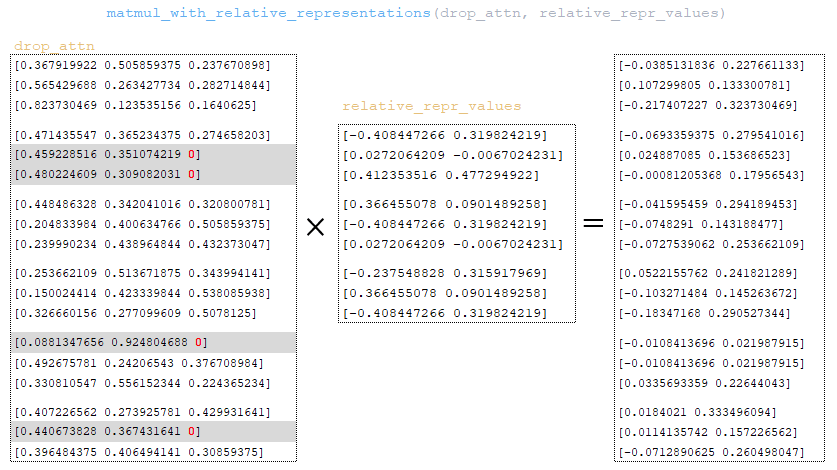
Матрица, полученная на шаге matmul_with_relative_representations, добавляется к матрице heads. (Изображение 31 - матрица heads)

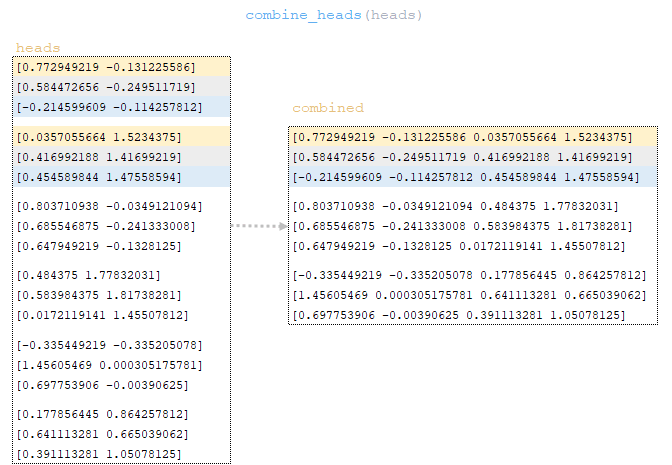
Матрица heads преобразуется в размерность исходной партии с помощью функции combine_heads - т. е. выполняются обратные операции split_heads - получается матрица combined. (Изображение 32 - матрица combined)
Матрица combined подвергается линейному преобразованию, после чего мы получаем матрицу outputs → outputs = linear_output (combined). Линейное преобразование полностью идентично с 1-го по 8-й шаг, описанный в классе Dense(). (Изображение 33 - линейное преобразование объединенной матрицы)

К outputs матрице применяется dropout (параметр dropout из файла конфигурации). (Изображение 34 - применение dropout к выходным матрицам)
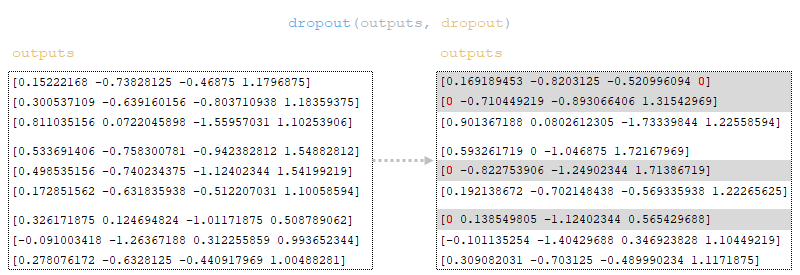
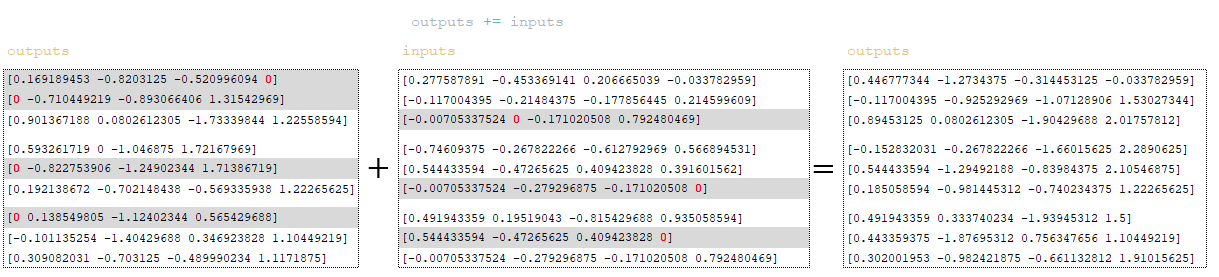
Применяется механизм остаточных связей ( residual connection) - матрица inputs добавляется к матрице outputs. Residual Connection - это механизм, используемый для решения проблемы исчезающего градиента в глубоких нейронных сетях и для улучшения обучения и сходимости модели. (Изображение 35 - outputs + inputs матрицы)
Матрица выходов передается в сеть прямого распространения ( Feed Forward Network ):
━ 1) применяется слой нормализации LayerNorm ();
━ 2) линейное преобразование класса Dense();
━ 3) Линейное преобразование с функцией активации ReLU tf.nn.relu
━ 4) применяется dropout (параметр ffn_dropout из файла конфигурации);
━ 5) линейное преобразование класса Dense();
━ 6) применяется dropout (параметр dropout из файла конфигурации);
━ 7) применяется механизм остаточной связи ( Residual connection).
(Изображение 36 - передача матрицы выходов в сеть прямого распространения)
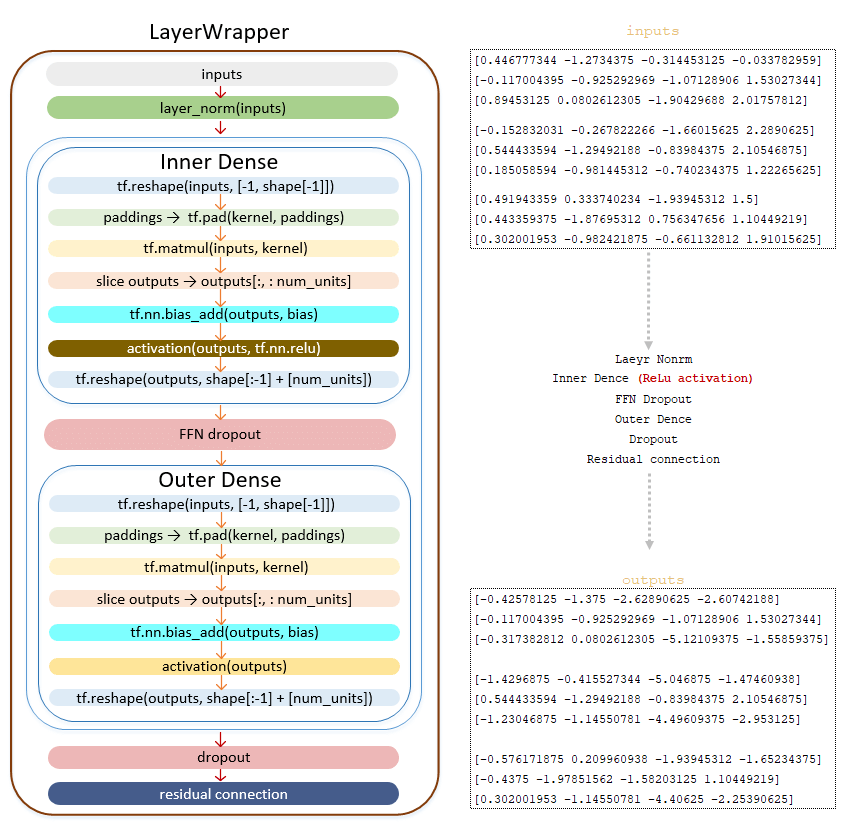
Если значение Layers больше единицы, то после преобразования outputs матрицы с помощью сети прямого распространения полученная матрица отправляется на вход следующего слоя, пока не пройдет все слои.
Полученная матрица выходов с последнего слоя проходит слой нормализации LayerNorm () - заключительную операцию в кодере. Полученная на этом этапе матрица передается в декодер. (Изображение 37 - слой нормализации LayerNorm ())
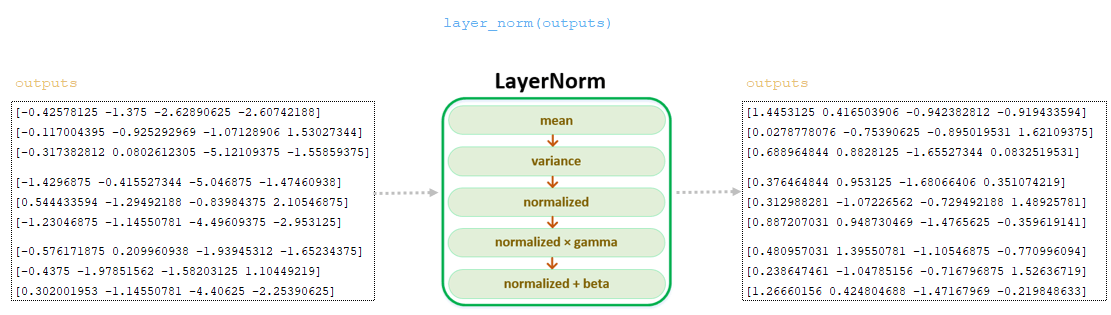
Описанный выше механизм преобразования пакетов токенов исходного языка в кодировщике можно отобразить следующим образом. (Изображение 38 - механизм преобразования токенизации исходного языка в кодировщик)
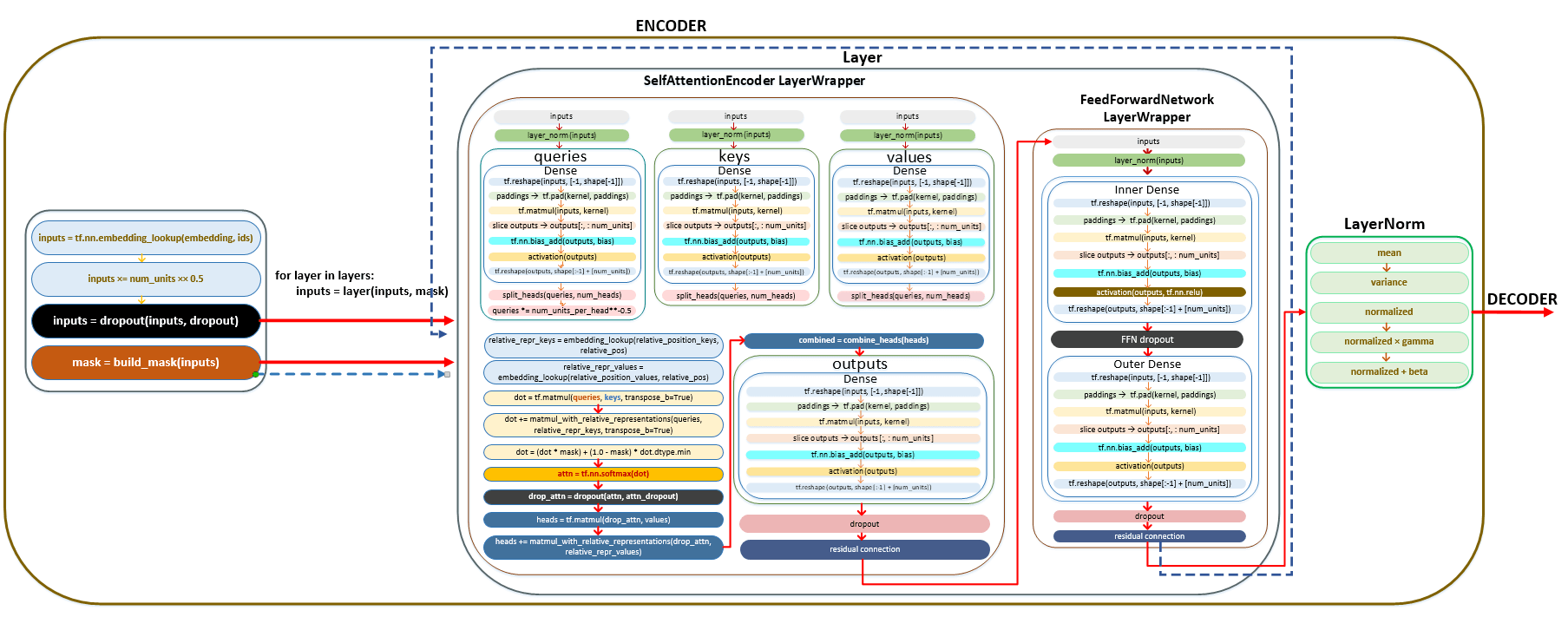
Кодер. Упрощенная последовательность вызова:
├──def call() | class Model(tf.keras.layers.Layer) модуль model.py
├──def call() | class SequenceToSequence(model.SequenceGenerator) модуль sequence_to_sequence.py
├──def call() | class WordEmbedder(TextInputter) модуль text_inputter.py
├──def call() | class SelfAttentionEncoder(Encoder) модуль self_attention_encoder.py
├──def build_mask() | class Encoder(tf.keras.layers.Layer) модуль encoder.py
├──def call() | class LayerWrapper(tf.keras.layers.Layer) модуль layers /common.py
├──def call() | class SelfAttentionEncoderLayer(tf.keras.layers.Layer) модуль layers/transformer.py
├──def call() | class MultiHeadAttention(tf.keras.layers.Layer)модуль layers/transformer.py
├──def call() | class Dense(tf.keras.layers.Dense) модуль layers /common.py
├──def call() | class LayerWrapper(tf.keras.layers.Layer) модуль layers /common.py
├──def call() | class FeedForwardNetwork(tf.keras.layers.Layer) модуль layers/transformer.py
├──def call() | class LayerNorm(tf.keras.layers.LayerNormalization) модуль layers/common.py
Заключение
В статье представлен всесторонний обзор функции кодировщика в нейронной сети, подробно описаны различные этапы обработки входных данных. В ней описывается, как завершается набор данных и как происходит обучение в пакетах, подчеркивая важность таких механизмов, как embedding, dropout и нормализация. На протяжении всего процесса подчеркивается использование многоголового внимания, демонстрируя, как queries, keys, and values матрицы преобразуются и объединяются. В статье также объясняется применение относительного позиционного кодирования и вычислений скалярного произведения, необходимых для механизмов внимания.
В конечном счете, выходные данные кодировщика дополнительно обрабатываются посредством нормализации и сети прямой связи с остаточными связями, обеспечивающими эффективное обучение. Затем окончательные выходные данные кодировщика подготавливаются для декодера, иллюстрируя критическую роль кодировщика в преобразовании входных токенов в значимые представления для последующей обработки.



