В этой статье рассматриваются несколько передовых техник, которые помогают повысить эффективность и результативность обучения моделей. Мы поговорим о методах, которые способствуют постепенной настройке параметров модели, что может привести к более стабильным процессам обучения. Эти техники позволяют тонко настроить процесс обновления весов модели, что улучшает сходимость и в конечном итоге дает лучшие результаты.
Кроме того, в статье обсуждаются стратегии управления темпами обучения, которые играют ключевую роль в том, насколько быстро модель обучается. Понимание того, как правильно корректировать темп обучения с течением времени, может существенно повлиять на динамику обучения и сделать модели более быстрыми и точными.
Наконец, мы затронем важность управления контрольными точками, что позволяет эффективнее использовать обученные модели, усредняя веса из нескольких сессий обучения. Это помогает снизить риск переобучения и обеспечивает сохранение лучших характеристик модели, приобретенных в процессе обучения.
Экспоненциальное скользящее среднее
В стандартной конфигурации модели типа транформер параметр moving_average_decay не задан. Установив его в значение, близкое к единице (согласно документации TensorFlow), следующим шагом будет вычисление экспоненциального скользящего среднего весов модели. Применение moving_average_decay к весам модели может значительно улучшить результаты работы модели.
Алгоритм работы moving_average_decay следующий:
- На каждом шаге обучения, после вычисления и применения градиентов, инициализируется класс MovingAverage;
- После инициализации MovingAverage вызывается функция для обновления весов модели.;
- Обновление весов происходит следующим образом:
- Рассчитывается коэффициент затухания:: decay = 1 - min(0.9999, (1.0 + training_step) / (10.0 + training_step))
- Для каждого веса модели применяется алгоритм: shadow_weigth = previous_weight - (previous_weight - current_weight) * decay (на первом шаге previous_weight = current_weight)
- Сглаженные веса сохраняются в классе MovingAverage после каждого шага обучения, а замена исходных весов на сглаженные происходит только при сохранении контрольной точки модели (Image 1 - ExponentialMovingAverage)

Упрощенная последовательность вызовов:
├── def call() class Trainer module training.py
├── def init() class MovingAverage module training.py
├── def _update_moving_average() class Trainer module training.py
├── def update() class MovingAverage module training.py
Механизм снижения темпа обучения
Механизм снижения темпа обучения использует переменные, инициализированные в классах NoamDecay и ScheduleWrapper classes.
После каждого шага обучения в классе ScheduleWrapper class: происходят следующие преобразования:
- Рассчитывается переменная step с использованием функции tf.math.maximum → tf.maximum(step - step_start, 0) = 1;
- Переменная step делится на step_duration с помощью целочисленного деления → step //= step_duration = 1 // 1 = 1;
- Значение step передается в класс NoamDecay.
В классе NoamDecay происходят следующие преобразования:
- Вычисляется переменная step → step = step + 1 = 2;
- Промежуточное значение a: с помощью функции tf.math.pow возводится в степень -0.5, что эквивалентно единице, деленной на квадратный корень из model_dim → 1 / sqrt(4) = 0.5;
- Промежуточное значение b: с помощью функции tf.pow function the step value obtained above is raised to the power of -0.5, что эквивалентно единице, деленной на квадратный корень из square root step → 1 / sqrt(2) = 0.7071;
- Промежуточное значение c: с помощью функции tf.pow значение warmup_steps возводится в степень -1.5 и умножается на значение step value → (1 / 8000^1.5) * 2 = 0.000001397 * 2 = 0.000002795;
- С помощью функции tf.math.minimum определяется минимальное значение между двумя промежуточными значениями b и c is determined → min(b, c) → 0.000002795;
- Полученное минимальное значение умножается на промежуточное значение a и scale → 0.0000027951 * 0.5 * 2 = 0.000002795;
- Полный цикл промежуточных преобразований выглядит так: (scale * tf.pow(model_dim, -0.5) * tf.minimum(tf.pow(step, -0.5), step * tf.pow(warmup_steps, -1.5)));
- Значение, полученное выше 0.000002795, возвращается обратно в класс ScheduleWrapper
В классе ScheduleWrapper рассчитывается окончательное значение коэффициента: learning rate = tf.maximum(learning_rate, minimum_learning_rate) → learning rate = max(0.000002795, 0.0001) = 0.000002795 = 0.0001. Это значение выводится в журнал обучения: Step = 1; Learning rate = 0.000100; Loss = 3.386743.
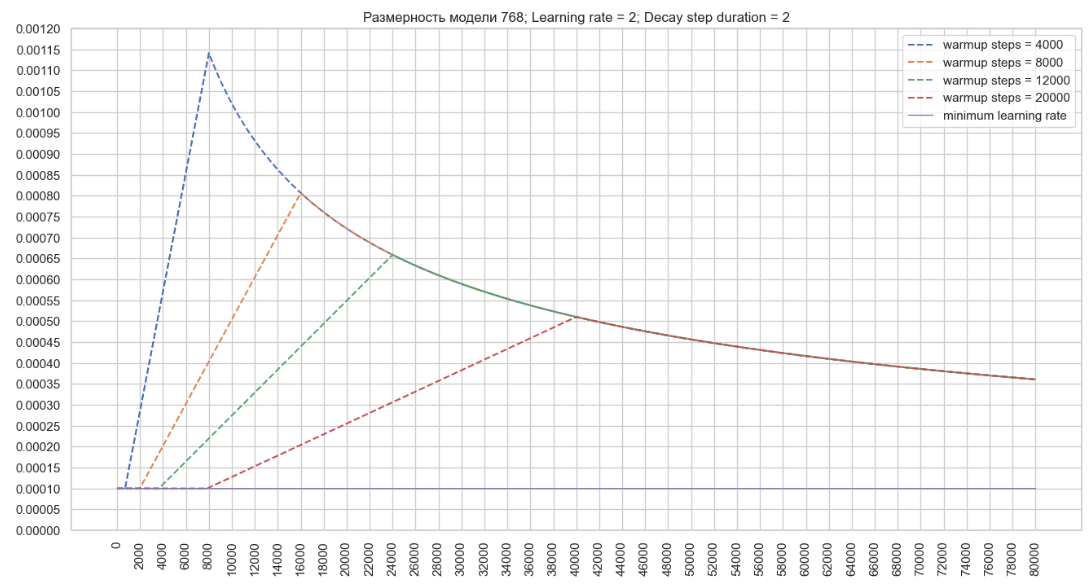
Используя описанный выше алгоритм, мы построим график изменений значения темпа обучения оптимизатора для модели с размерностью 768 и указанным параметром Learning rate = 2 в конфигурационном файле тренера. (Image 2 - Learning rate = 2)
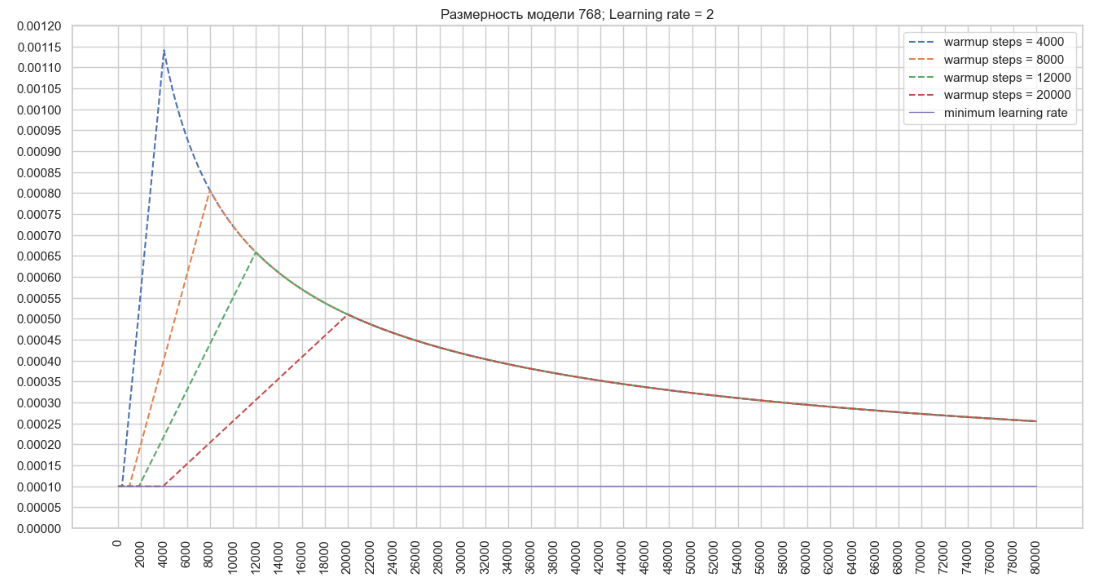
Теперь давайте построим график изменений значения темпа обучения оптимизатора для модели с размерностью 768 и указанным параметром Learning rate = 6 в конфигурационном файле тренера. (Image 3 - Learning rate = 6 )
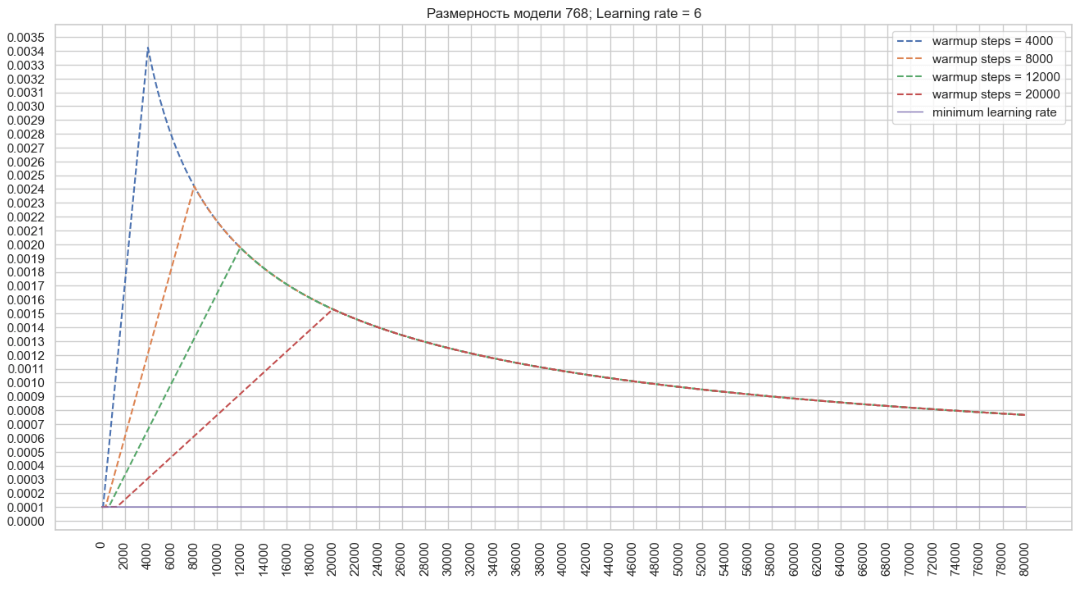
Исходя из этого можно сделать вывод, что при снижении значения warmup_steps темп обучения оптимизатора растет быстро, в то время как увеличение значения в конфигурации позволяет достичь более высоких значений learning rate оптимизатора, что может ускорить обучение при большой размерности модели.
Кроме того, на изменение темпа обучения можно повлиять с помощью параметра start_decay_steps. Это позволяет задать количество шагов, после которых начнется применение механизма warmup_steps и последующего снижения темпа обучения.
На следующем графике видно, что при start_decay_steps = 10,000, в первые 10 тысяч шагов модель обучается с фиксированным минимальным темпом обучения, а после этого начинает работать механизм warmup_steps с последующим снижением. (Image 4 - start_decay_steps = 10 000)
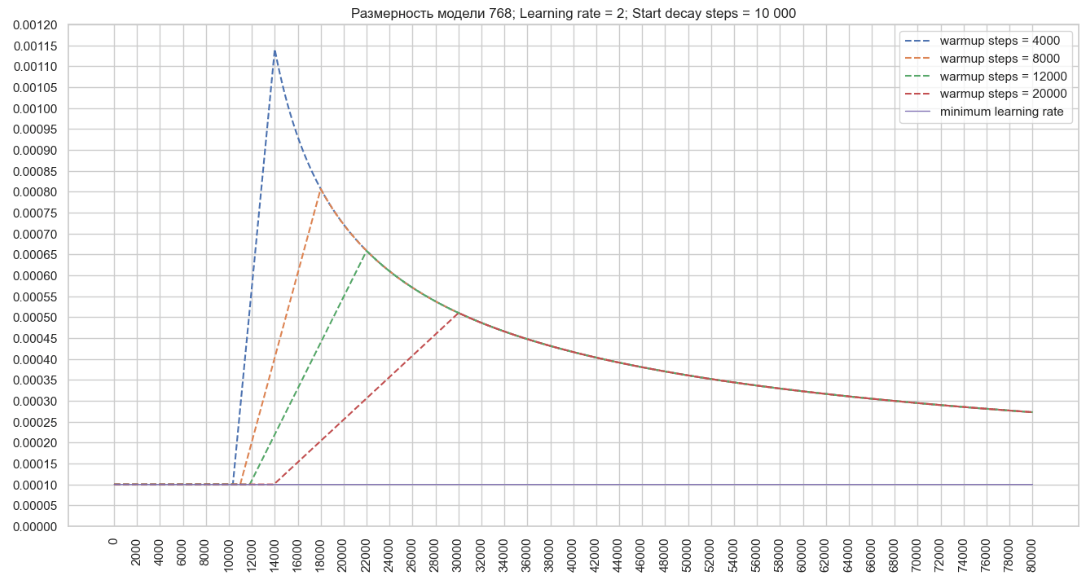
Параметр decay_step_duration можно использовать для увеличения продолжительности механизма warmup_steps и замедления темпа снижения. (рис. 5 - decay_step_duration)
Упрощенная последовательность вызовов:
├── def call() class ScheduleWrapper module schedules/lr_schedules.py
├── def call() class class NoamDecay module schedules/lr_schedules.py
├── def call() class ScheduleWrapper module schedules/lr_schedules.py
Механизм усреднения контрольных точек
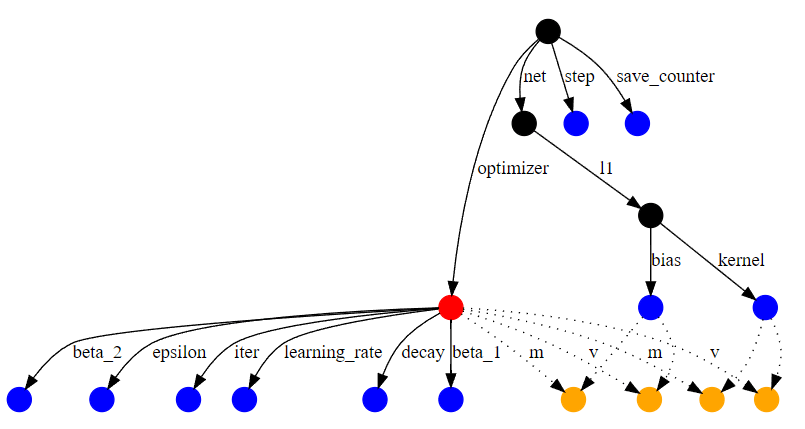
Контрольная точка (checkpoint) — это состояние модели на определенном шаге обучения. Контрольная точка обученной модели сохраняет веса модели, измененные во время обучения, переменные оптимизатора для каждого слоя (состояние оптимизатора на определенном шаге обучения) и граф вычислений. Пример небольшого графа вычислений для простой сети показан на рис. 6 (Рис. 6 — Граф вычислений). Оптимизатор выделен красным, обычные переменные — синим, а переменные слотов оптимизатора — оранжевым. Другие узлы выделены черным. Переменные слотов являются частью состояния оптимизатора, но создаются для конкретной переменной. Например, ‘m’ на ребрах выше соответствует моментуму, который оптимизатор Adam отслеживает для каждой переменной.
В конце обучения восстанавливаются последние контрольные точки модели, количество которых соответствует значению параметра average_last_checkpoints parameter.
Согласно архитектуре обученной модели, веса инициализируются значением ноль для всех слоев модели.
Далее в цикле для каждой восстановленной контрольной точки считываются веса; веса каждого слоя делятся на количество контрольных точек, указанное в параметре average_last_checkpoints, и полученные значения добавляются к весам, инициализированным выше, с помощью функции variable.assign_add(value / num_checkpoints) (слой embeddings суммируется только с самим слоем embeddings и т. д.).
Механизм усреднения для небольшого слоя из нашего примера модели, с усреднением последних двух контрольных точек, показан на рис. 7. (Рис. 7 — Усреднение последних двух контрольных точек)

Заключение
В завершение, техники, рассмотренные в этой статье, дают ценную информацию для оптимизации обучения глубоких нейронных сетей. Применяя стратегии для настройки весов, управления темпом обучения и усреднения контрольных точек, можно значительно повысить производительность и стабильность модели.
Эти методы не только делают процесс обучения более плавным, но и помогают достичь лучшей сходимости и обобщения. В конечном итоге, понимание и использование этих концепций позволит исследователям улучшить свои рабочие процессы и сделать решения в области машинного обучения более эффективными и результативными.



