Статья предоставляет всесторонний обзор вычисления функции потерь в машинном обучении, особенно в контексте моделей последовательностей. Она начинается с подробного описания того, как матрица логитов, генерируемая после преобразований в декодере, обрабатывается через функцию cross_entropy_sequence_loss. Эта функция играет ключевую роль в измерении расхождения между предсказанными выводами и фактическими метками. В статье описаны шаги, включая преобразование логитов в подходящий формат, применение сглаживания меток для создания сглаженных меток и вычисление кросс-энтропийных потерь с использованием softmax. Каждый этап подробно объясняется, чтобы было понятно, как каждый компонент вносит вклад в общую оценку потерь.
Кроме вычисления потерь, статья рассматривает механизм выравнивания, используемый для улучшения работы модели. Описано, как значение потерь корректируется на основе направляемого выравнивания, что позволяет модели лучше учитывать взаимосвязи между исходными и целевыми последовательностями. Также подробно рассматривается процесс вычисления и применения градиентов, иллюстрируя, как оптимизатор обновляет веса модели для минимизации потерь.

Расчет функции потерь
Процесс начинается с матрицы логитов, полученной после преобразований в декодере, и передается в функцию cross_entropy_sequence_loss для пакета целевого языка. (Изображение 1 - матрица логитов)

Внутри функции выполняются следующие преобразования:
1) вычисляется матрица cross_entropy с использованием функции softmax_cross_entropy
- значения матрицы логитов преобразуются в тип float32 с помощью функции tf.cast → logits = tf.cast(logits, tf.float32);
- значение переменной num_classes вычисляется по размерности матрицы логитов → num_classes = logits.shape[-1] ; так как размерность матрицы логитов равна [3, 4, 26], значение переменной будет равно 26;
- on_value → 1.0 - label_smoothing (параметр label_smoothing берется из конфигурации обучения); значение переменной будет равно 0.9;
- off_value рассчитывается как → label_smoothing / (num_classes - 1 ) ; 1/(26 - 1) = 0.004;
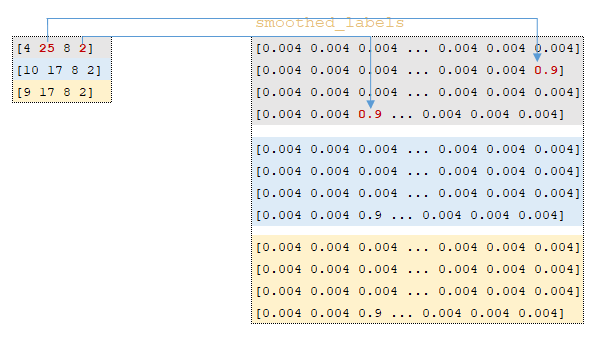
- используя функцию tf.one_hot вычисляется матрица смещенных метрик smoothed_labels → tf.one_hot(labels, 26, 0.9, 0.004); Эта трансформация работает следующим образом: индексы выходных токенов ids_out извлекаются из пакетов токенов целевого языка, строится матрица с глубиной 26 элементов, и если индекс элемента в матрице совпадает с индексом из матрицы ids_out этот индекс заполняется значением on_value. Все остальные элементы заполняются значением off_value. (Изображение 2 - матрица смещенных метрик);
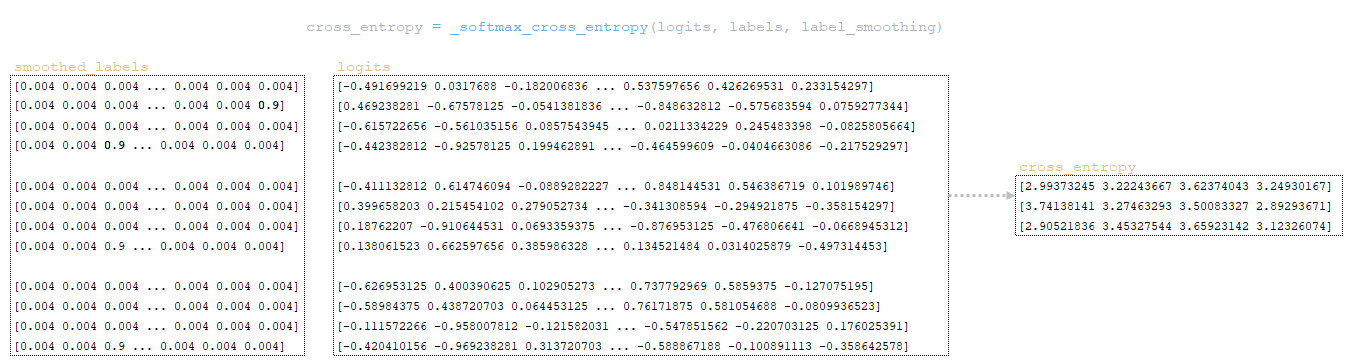
- функция tf.nn.softmax_cross_entropy_with_logits вычисляет кросс-энтропию softmax между матрицами smoothed_labels и logits matrices. Кросс-энтропия измеряет расхождение между двумя распределениями вероятностей.
Алгоритм этой функции следующий:
- вычисление экспоненты матрицы логитов - эквивалентно numpy.exp(logits);
- суммирование элементов матрицы по строкам - эквивалентно numpy.sum(numpy.exp(logits), axis=-1);
- вычисление десятичного логарифма полученной матрицы и ее транспортирование по размерности матрицы логитов (в нашем примере 3 x 4 x 1) эквивалентно numpy.log(numpy.sum(numpy.exp(logits), axis=-1)).reshape(3, 4, 1);
- вычитание матрицы, полученной на предыдущем шаге, из матрицы логитов, чтобы сформировать матрицу logsoftmax matrix → logsoftmax = logits - numpy.log(numpy.sum(numpy.exp(logits), axis=-1)).reshape(3, 4, 1)).reshape(3, 4, 1) ;
- вычисление матрицы кросс-энтропии — матрица logsoftmax умножается на отрицательную матрицу логитов, и результат суммируется по строкам → cross_entropy = numpy.sum(logsoftmax * -labels, axis=-1). (Изображение 3 - кросс-энтропия)
2) используя функцию tf.sequence_mask, вычисляется матрица weight использованием переменной sequence_length (которая содержит значения длины предложений в токенах, сгруппированных в батч) и размерности матрицы logits.shape[1] [3, 4, 26]; (Изображение 4 -матрица weight)

3) используя функцию tf.math.reduce_sum, вычисляется переменная loss → loss = tf.reduce_sum( cross_entropy * weight ) = 39.6399841 результат произведения матриц cross_entropy и weight; (Изображение 5 - продукт произведение матриц cross-entropy и weight)

4) используя функцию tf.math.reduce_sum вычисляется переменная loss_token_normalizer с использованием матрицы weight, которая будет равна количеству токенов в батче → loss_token_normalizer = tf.reduce_sum(weight) = 12;
5) в результате возвращаются два значения: loss = 39.6399841 и loss_token_normalizer = 12.
Упрощенная последовательность вызовов:
├── def _accumulate_gradients(self, batch) модуль training.py
├── def compute_gradients(features, labels, optimizer) class Model(tf.keras.layers.Layer) модуль model.py
├── def compute_training_loss(features, labels) class Model(tf.keras.layers.Layer) модуль model.py
├── def compute_loss(outputs, labels) class SequenceToSequence(model.SequenceGenerator) модуль sequence_to_sequence.py
├── def cross_entropy_sequence_loss() модуль utils/losses.py
Механизм выравнивания
При обучении модели с выравниванием, значение переменной loss полученной на предыдущем шаге, корректируется с использованием функции guided_alignment_cost. Внутри этой функции происходят следующие преобразования:
1) в зависимости от параметра типа выравнивания - Guided alignment type, установленного в конфигурационном файле, определяется функция преобразования:
- для значения ce - tf.keras.losses.CategoricalCrossentropy(reduction=tf.keras.losses.Reduction.SUM) - значение по умолчанию
- для значения mse - tf.keras.losses.MeanSquaredError(reduction=tf.keras.losses.Reduction.SUM)
2) Рассчитывается длина предложений в токенах по батчам токенов целевого языка; (Изображение 6 - get_length)

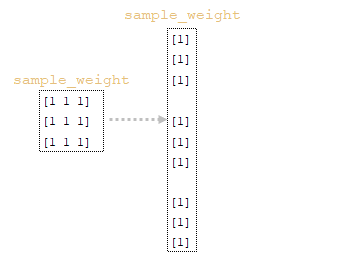
3) используя функцию tf.sequence_mask, строится тензор весов с использованием полученных длин предложений и размерности матрицы attention tf.shape(attention)[1]; Для нашего примера длина предложений в токенах будет [3 3 3 3] а размерность матрицы attention [3 3 3 3]; (Изображение 7 - sample_weight)

4) с помощью функции tf.expand_dims(input, axis) матрица sample_weight меняет свою форму → sample_weight = tf.expand_dims(sample_weight, -1); (Изображение 8 - видоизмененная матрица sample_weight)
5) используя функцию tf.reduce_sum, вычисляется нормализатор → normalizer = tf.reduce_sum([3 3 3 3]) = 9 из массива длин батчей предложений;
6) с помощью функции tf.keras.losses.CategoricalCrossentropy(alignment, attention), рассчитывается значение переменной cost используя матрицы alinement и sample_weight (матрица attention (последний элемент attention[:, :-1] в каждом векторе представления токенов из матрицы attention удален заранее, чтобы размерности совпали, так как размерность начальной матрицы attention равна 3 x 4 x 3)); (Изображение 9 - расчет значения переменной cost)
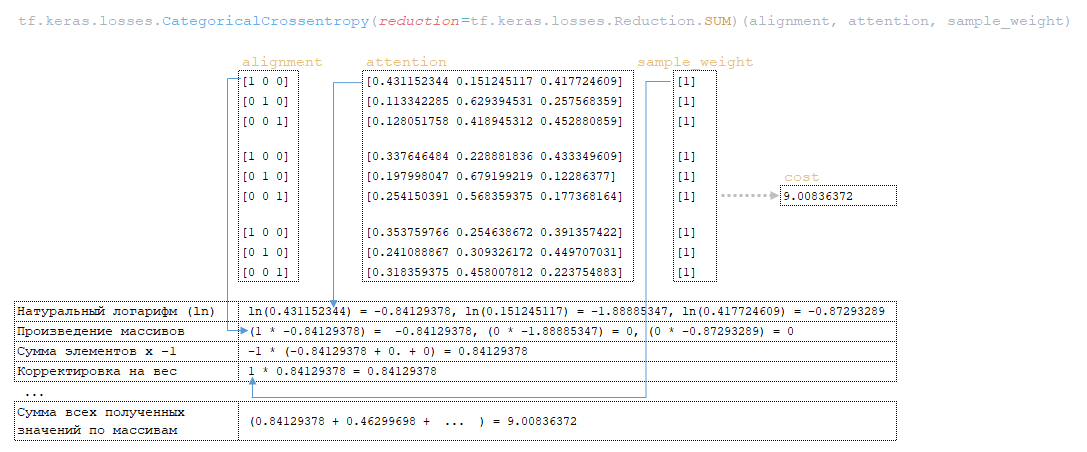
7) переменная cost делится на переменную normalizer → cost = cost / normalizer = 9.00836372 / 9 = 1.00092936 ;
8) переменная cost умножается на значение переменной weight (параметр из конфигурационного файла Guided alignment weight ) → cost = cost * weight = 1.00092936 * 1 = 1.00092936 ;
9) значение переменной loss полученное в функции cross_entropy_sequence_loss корректируется на значение переменной cost путем сложения loss = loss + cost = 39.6399841 + 1.00092936 = 40.6409149.
Упрощенная последовательность вызовов:
├── def _accumulate_gradients(self, batch) модуль training.py
├── def compute_gradients(features, labels, optimizer) class Model(tf.keras.layers.Layer) модуль model.py
├── def compute_training_loss(features, labels) class Model(tf.keras.layers.Layer) модуль model.py
├── def compute_loss(outputs, labels) class SequenceToSequence(model.SequenceGenerator) модуль sequence_to_sequence.py
├── def guided_alignment_cost() модуль utils/losses.py
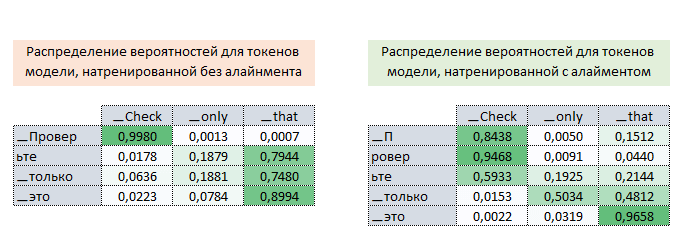
Таким образом, в процессе обучения модели с выравниванием, мы корректируем значение функции потерь (увеличивая его) и таким образом “заставляем”оптимизатор минимизировать функцию потерь с учетом влияния выравнивания. На рисунке ниже показаны распределения вероятностей матриц attention токенов целевого языка к токенам исходного языка для полностью обученных моделей без выравнивания и с выравниванием.
Распределения показывают, что по вероятностям матрицы внимания моделей с выравниванием токены [▁П, ровер, ьте] могут быть правильно сопоставлены с токеном ▁Check, в то время как по матрице внимания моделей без выравнивания это сделать невозможно. (Изображение 10 - матрица с выравниванием и без выравнивания)
Механизм расчета и применения градиентов
Процесс расчета и применения градиентов включает следующие шаги:
- Полученное значение функции потерь корректируется с учетом значения loss_scale (первоначально равного 32,768) класса оптимизатора LazyAdam: scaled_loss = optimizer.get_scaled_loss(loss) → scaled_loss = 40.640914 * 32,768 = 1,331,721.5
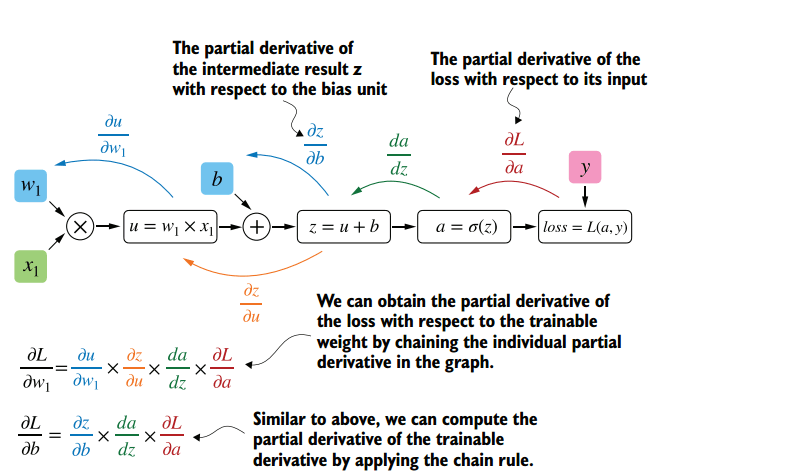
- на основе значения scaled_loss и параметров модели trainable_weights градиенты рассчитываются с использованием функции gradient класса tf.GradientTape. Градиенты являются производными по весам модели. Расчет основан на алгоритме обратного распространения ошибки.
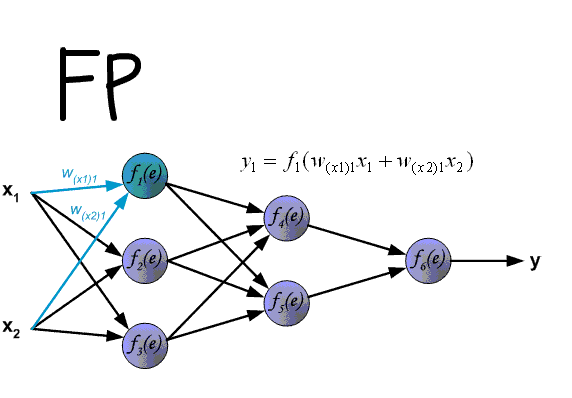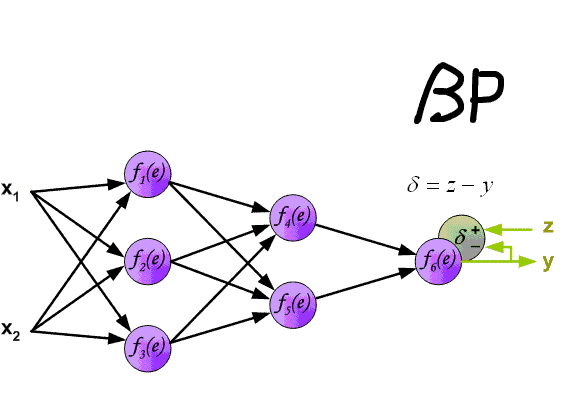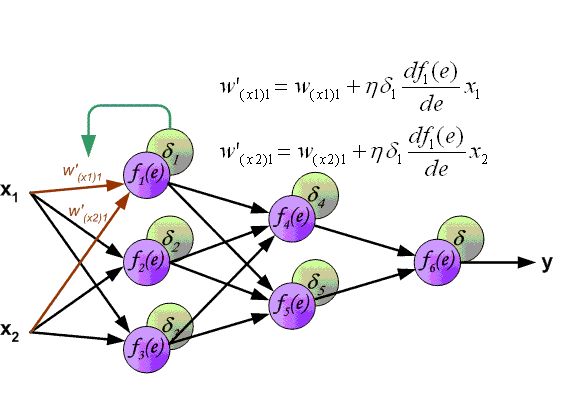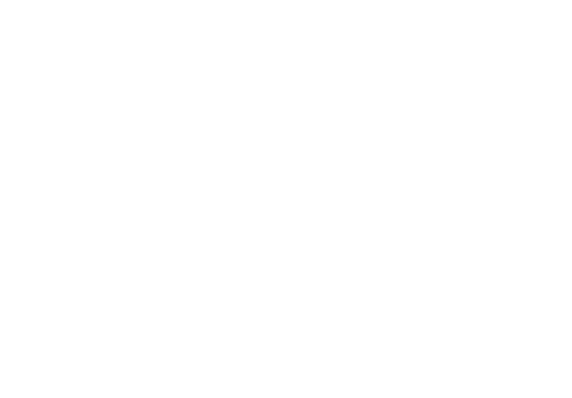
Суть этого метода заключается в том, что на основе полученного значения scaled_loss и матрицы весов модели trainable_weights, вычисляются производные по весам модели слева направо по всему графу вычислений. That is, То есть мы берем значение функции потерь scaled_loss и находим производные для значений, полученных на выходе декодера, затем для значений, полученных в энкодере, и так далее, вплоть до начальных значений модели. Цель состоит в том, чтобы найти значения производных таким образом, чтобы минимизировать функцию потерь. Концептуально, схема обучения нейронной сети выглядит следующим образом: функция потерь принимает минимальное значение → мы находим веса, соответствующие этому значению → ошибка минимальна → точное предсказание нейронной сети. Визуально схема расчета вектора градиентов и механизма обратного распространения ошибки может быть представлена следующим образом.
(Изображение 11 - расчет вектора градиентов)
(Изображение 12 - механизма обратного распространения ошибки )
- при обучении модели смешанной точности (FP16), градиенты делятся на значение loss_scale используя функцию оптимизатора optimizer.get_unscaled_gradients(gradients); ниже представлен фрагмент весов модели и соответствующих градиентов начало и конец матрицы; (Изображение 13 - фрагмент модели весов и соответствующих градиентов)

- таким образом, мы получаем матрицу градиентов, размер которой будет равен размеру матрицы весов модели, т.е. если в модели 1 миллион параметров, то матрица градиентов будет содержать 1 миллион значений;
- После расчета матрицы градиентов для всех групп (батчей) градиенты накапливаются. Например, при эффективном размере батча = 200,000 и размере батча = 6,250. количество групп будет равно 32, то есть после подсчета градиентов, у нас будет 32 матрицы градиентов - каждый батч имеет свою собственную градиентную матрицу. Градиенты накапливаются путем сложения этих матриц. Помимо накопления матриц градиентов, так же накапливаются значения, полученные в функции потерь loss и loss_token_normalizer (общее количество целевых токенов в батче) с формированием следующих переменных:
━ loss = all_reduce_sum(loss)
━ sample_size = all_reduce_sum(loss_token_normalizer)
- После того как матрицы градиентов, loss и loss_token_normalizer суммированы значение градиента делится на общее количество токенов в группе sample_size. Например, ниже представлена схема для трех батчей с общим числом токенов 146 ; (Изображение 14 - схема для трех батчей с общим числом токенов)

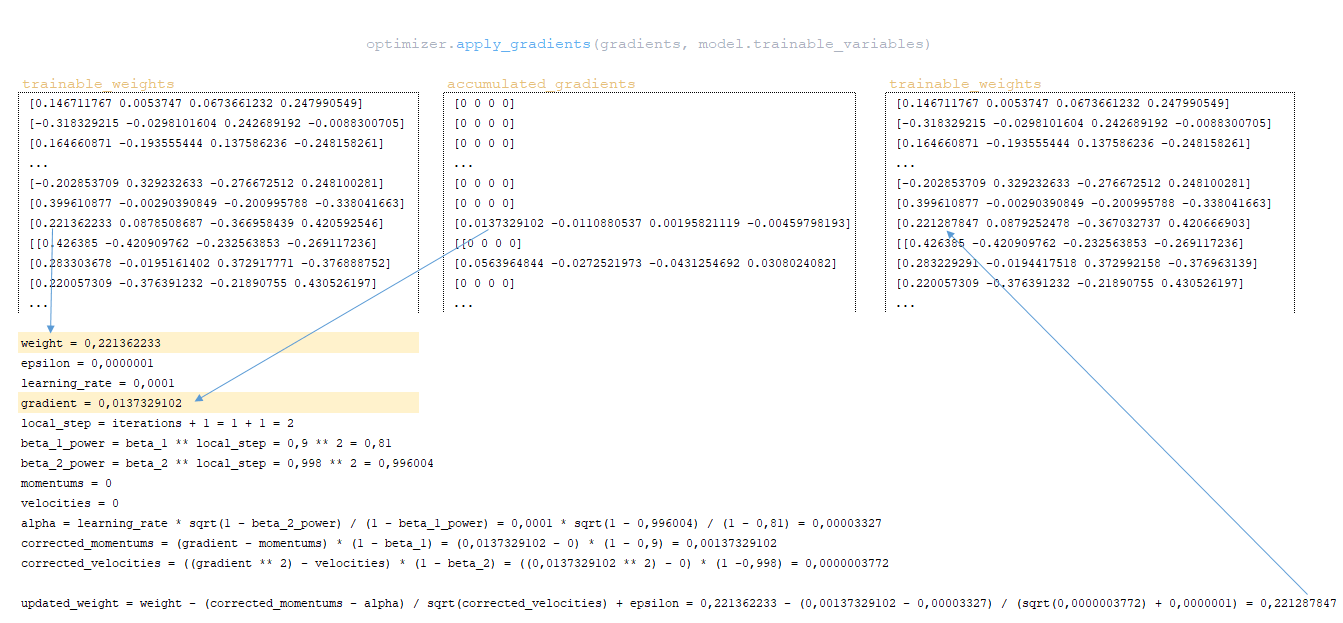
- с помощью функции apply_gradients класса оптимизатора, градиенты применяются к весам модели, то есть веса модели обновляются. Реализация механизма обновления весов Adam включает:
━ momentums и velocities - изначально инициализируются нулями. Они содержат значения моментов для каждого веса модели и будут корректироваться и обновляться с каждым шагом;
━ alpha - адаптивное значение параметра learning rate.
(Изображение 15 -применение градиентов к весам модели)
При использовании другого типа оптимизатора механизм расчета и применения градиентов будет отличаться.
Упрощенная последовательность вызовов:
├── def call() class Trainer модуль training.py
├── def _steps() class Trainer модуль training.py
├── def _accumulate_gradients(batch) class Trainer модуль training.py
├── def compute_gradients() class Model(tf.keras.layers.Layer) модуль model.py
├── def _accumulate_loss() class Trainer модуль training.py
├── def call() class GradientAccumulator модуль optimizers/utils.py
├── def _apply_gradientss() class Trainer модуль training.py
После применения градиентов, значение функции потерь делится на общее количество токенов: loss = float(loss) / float(sample_size) → 40.6409149 / 12 = 3.38674291. Именно это значение будет отображаться в журнале обучения: Step = 1; Loss = 3.386743. Кроме того, это значение будет использоваться для построения графика функции потерь обучения, который отображается в TensorBoard.
Заключение
Статья завершена выделением ключевых процессов, связанных с вычислением потерь и применением градиентов в моделях машинного обучения. Понимание того, как взаимодействуют эти компоненты, особенно корректировки для выравнивания и тщательное вычисление градиентов, позволяет исследователям лучше оптимизировать свои модели для повышения точности и производительности.