L'article offre une vue d'ensemble complète sur le calcul des fonctions de perte en apprentissage automatique, en particulier dans le contexte des modèles de séquences. Il commence par expliquer comment la matrice des logits, générée après les transformations effectuées dans le décodeur, est traitée à travers la fonction cross_entropy_sequence_loss. Cette fonction joue un rôle clé en mesurant l'écart entre les prédictions du modèle et les étiquettes réelles. Les étapes incluent la conversion des logits dans un format approprié, l'application du lissage des étiquettes pour générer des étiquettes lissées, et le calcul de la perte par entropie croisée en utilisant la fonction softmax. Chaque transformation est expliquée en détail, rendant clair le rôle de chaque composant dans l'évaluation globale de la perte.
En plus du calcul de la perte, l'article examine le mécanisme d'alignement utilisé pour améliorer les performances du modèle. Il décrit comment la valeur de la perte est ajustée en fonction d'un alignement guidé, permettant au modèle de mieux prendre en compte les relations entre les séquences source et cible. Le processus de calcul et d'application des gradients est également détaillé, illustrant comment l'optimiseur met à jour les weight du modèle pour minimiser la perte.

Calcul de la fonction de perte
Le processus débute avec la matrice des logits obtenue après les transformations dans le décodeur. Le lot de la langue cible est ensuite passé à la fonction cross_entropy_sequence_loss. (Image 1 - matrice des logits)

Les transformations suivantes ont lieu à l'intérieur de la fonction:
La matrice d'entropie croisée est calculée à l'aide de la fonction softmax_cross_entropy:
- Les valeurs de la matrice des logits sont converties au type float32 à l'aide de la fonction tf.cast → logits = tf.cast(logits, tf.float32) ;
- La valeur de la variable num_classes est calculée à partir de la dimension de la matrice des logits → num_classes = logits.shape[-1] ; étant donné que la dimension de la matrice des logits est [3, 4, 26], la valeur de la variable sera égale à 26 ;
- on_value → 1.0 - label_smoothing (le paramètre label_smoothing est défini dans la configuration d'entraînement) ; la valeur de cette variable sera égale à 0,9 ;
- La valeur de off_value est calculée → label_smoothing / (num_classes - 1) ; 1/(26 - 1) = 0,004 ;
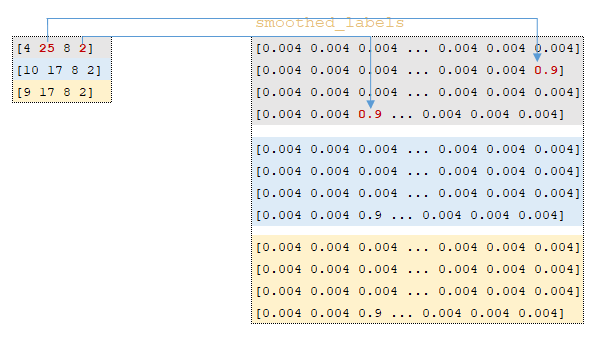
- À l'aide de la fonction tf.one_hot, la matrice smoothed_labels est calculée → tf.one_hot(labels, 26, 0.9, 0.004) ; cette transformation fonctionne de la manière suivante: les indices des tokens de sortie ids_out sont extraits des lots de tokens de la langue cible, une matrice avec une profondeur de 26 éléments est construite, et si l'indice d'un élément de la matrice correspond à l'indice de la matrice ids_out, cet indice est rempli avec la valeur de on_value. Tous les autres éléments sont remplis avec la valeur de off_value. (Image 2 - matrice smoothed_labels).
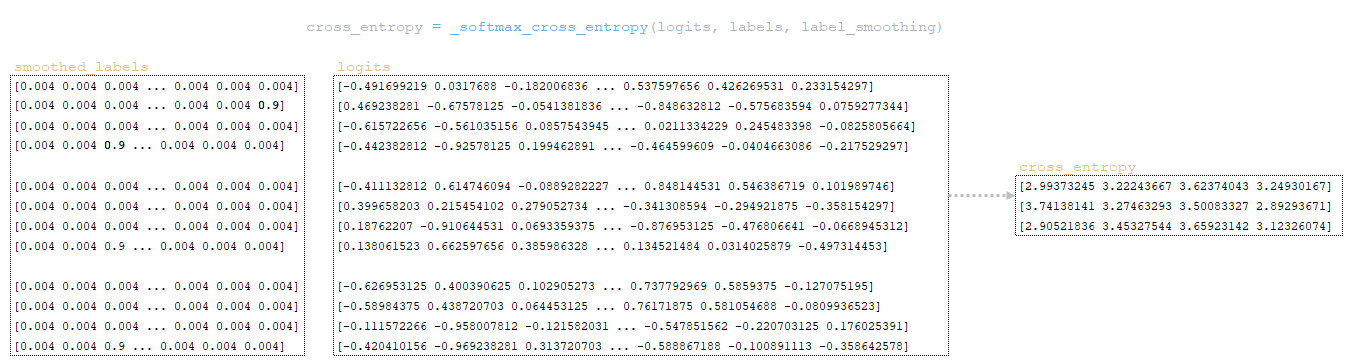
- La fonction tf.nn.softmax_cross_entropy_with_logits calcule l'entropie croisée softmax entre les matrices smoothed_labels et logits. L'entropie croisée mesure la différence entre deux distributions de probabilités.
L'algorithme de cette fonction est le suivant:
- L'exponentielle des éléments de la matrice logits est calculée — équivalent à numpy.exp(logits) ;
- Les éléments de la matrice résultante sont additionnés ligne par ligne — équivalent à numpy.sum(numpy.exp(logits), axis=-1) ;
- Le logarithme décimal de la matrice obtenue est calculé, puis transposé selon les dimensions de la matrice logits (dans notre exemple, 3 x 4 x 1) — équivalent à numpy.log(numpy.sum(numpy.exp(logits), axis=-1)).reshape(3, 4, 1) ;
- La matrice obtenue à l'étape précédente est soustraite de la matrice logits pour former la matrice logsoftmax → logsoftmax = logits - numpy.log(numpy.sum(numpy.exp(logits), axis=-1)).reshape(3, 4, 1) ;
- La matrice cross_entropy est calculée: la matrice logsoftmax est multipliée par la matrice négative des étiquettes, et le produit est ensuite additionné ligne par ligne → cross_entropy = numpy.sum(logsoftmax * -labels, axis=-1). (Image 3 - matrice cross_entropy).
2. À l'aide de la fonction tf.sequence_mask, la matrice de weight est calculée en utilisant la variable sequence_length. Cette variable contient les longueurs des phrases exprimées en nombre de tokens, regroupées par lot (batch). La dimension de la matrice est définie par logits.shape[1] [3, 4, 26]. (Image 4 - matrice de weight).

3. À l'aide de la fonction tf.math.reduce_sum, la variable loss est calculée: loss = tf.reduce_sum(cross_entropy * weight) = 39.6399841, en multipliant les matrices cross_entropy et weight. (Image 5 - produit des matrices cross_entropy et weight).

4. À l'aide de la fonction tf.math.reduce_sum, la variable loss_token_normalizer est calculée en utilisant la matrice de weight. Cette variable correspond au nombre total de tokens dans le lot → loss_token_normalizer = tf.reduce_sum(weight) = 12 ;
5. Le résultat retourne deux variables: loss = 39.6399841 et loss_token_normalizer = 12.
Séquence d'appels simplifiée:
├── def _accumulate_gradients(self, batch) dans le module training.py
├── def compute_gradients(features, labels, optimizer) class Model(tf.keras.layers.Layer) du module model.py
├── def compute_training_loss(features, labels) class Model(tf.keras.layers.Layer) du module model.py
├── def compute_loss(outputs, labels) class SequenceToSequence(model.SequenceGenerator) du module sequence_to_sequence.py
├── def cross_entropy_sequence_loss() dans le module utils/losses.py
Mécanisme d'alignement
Lors de l'entraînement d'un modèle avec un alignement, la valeur de la variable loss, obtenue à l'étape précédente, est ajustée en utilisant la fonction guided_alignment_cost. Les transformations suivantes ont lieu dans cette fonction:
1. Selon le paramètre Guided alignment type défini dans le fichier de configuration, la fonction de conversion est déterminée:
- Pour la valeur ce (valeur par défaut) - tf.keras.losses.CategoricalCrossentropy(reduction=tf.keras.losses.Reduction.SUM) ;
- Pour la valeur mse → tf.keras.losses.MeanSquaredError(reduction=tf.keras.losses.Reduction.SUM) ;
2. La longueur des phrases en tokens est calculée à partir des lots de tokens de la langue cible ; (Image 6 - get_length).

3. À l'aide de la fonction tf.sequence_mask, le tenseur de weight sample_weight est construit en utilisant les longueurs de phrases obtenues et la dimension de la matrice attention (tf.shape(attention)[1]). Dans notre exemple, les longueurs des phrases en tokens seront [3, 3, 3, 3], et la dimension de la matrice attention sera également [3, 3, 3, 3]. (Image 7 - sample_weight).

4. À l'aide de la fonction tf.expand_dims(input, axis), la matrice sample_weight est redimensionnée → sample_weight = tf.expand_dims(sample_weight, -1). (Image 8 - matrice sample_weight modifiée).
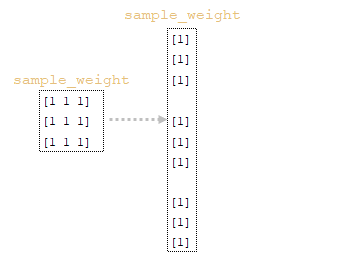
5. À l'aide de la fonction tf.reduce_sum, le normalisateur est calculé à partir du tableau des longueurs des phrases du lot → normalizer = tf.reduce_sum([3, 3, 3, 3]) = 9.
6. À l'aide de la fonction tf.keras.losses.CategoricalCrossentropy(alignment, attention), la valeur de la variable cost est calculée en utilisant la matrice alignment (pour laquelle la dernière ligne de chaque représentation vectorielle des tokens dans la matrice attention a été retirée, i.e., attention[:,:-1], afin que les dimensions des matrices correspondent, car la dimension initiale de la matrice attention est 3 x 4 x 3) et la matrice sample_weight. (Image 9 - calcul de la variable cost).
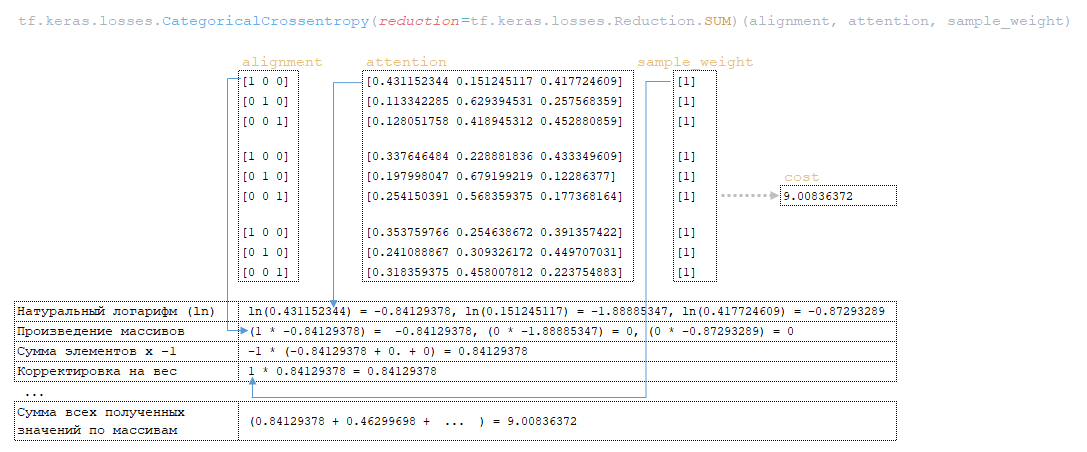
7. La variable cost est divisée par la variable normalizer → cost = cost / normalizer = 9.00836372 / 9 = 1.00092936.
8. La variable cost est ensuite multipliée par la valeur de la variable weight (paramètre provenant du fichier de configuration Guided alignment weight ) → cost = cost * weight = 1.00092936 * 1 = 1.00092936.
9. La valeur de la variable loss, obtenue dans la fonction cross_entropy_sequence_loss, est ajustée en ajoutant la valeur de la variable cost → loss = loss + cost = 39.6399841 + 1.00092936 = 40.6409149.
Séquence d'appels simplifiée:
├── def _accumulate_gradients(self, batch) dans le module training.py
├── def compute_gradients(features, labels, optimizer) class Model(tf.keras.layers.Layer) du module model.py
├── def compute_training_loss(features, labels) class Model(tf.keras.layers.Layer) du module model.py
├── def compute_loss(outputs, labels) class SequenceToSequence(model.SequenceGenerator) du module sequence_to_sequence.py
├── def guided_alignment_cost() dans le module utils/losses.py
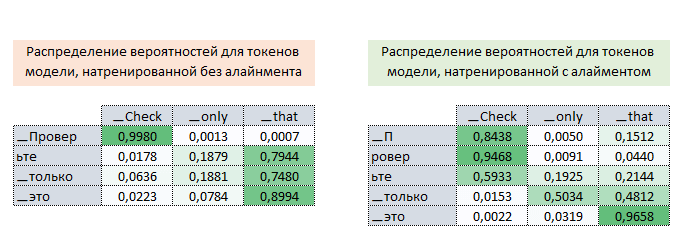
Ainsi, de manière itérative, pendant l'entraînement du modèle avec un alignement, la valeur de la fonction de perte est ajustée (en augmentant sa valeur), ce qui "force" l'optimiseur à minimiser cette fonction tout en tenant compte de l'influence de l'alignement. L'image ci-dessous montre les distributions de probabilités des matrices d'attention des tokens de la langue cible par rapport aux tokens de la langue source, pour des modèles entièrement entraînés avec et sans alignement.
Ces distributions démontrent qu'avec les probabilités de la matrice d'attention des modèles avec alignement, les tokens [▁П, ровер, ьте] peuvent être correctement associés au token ▁Check. En revanche, avec la matrice d'attention des modèles sans alignement, cette correspondance n'est pas possible. (Image 10 - matrice avec et sans alignement).
Mécanisme de calcul et d'application des gradients
Le processus de calcul et d'application des gradients se déroule comme suit:
La valeur de perte obtenue est ajustée par la valeur de loss_scale (initialement définie à 32,768) de la classe LazyAdam de l'optimiseur:
scaled_loss = optimizer.get_scaled_loss(loss) →
scaled_loss = 40.640914 * 32,768 = 1,331,721.5.
À partir de la valeur de scaled_loss obtenue et des poids entraînables du modèle (trainable_weights), les gradients sont calculés à l'aide de la fonction gradient de la classe tf.GradientTape. Les gradients sont les dérivées par rapport aux poids du modèle. Le calcul des gradients est basé sur l'algorithme de rétropropagation (backpropagation), un processus complexe.
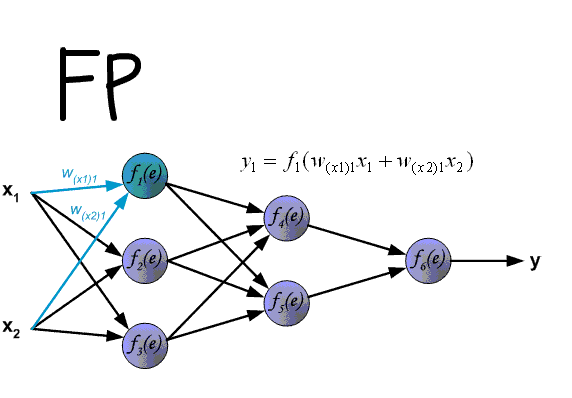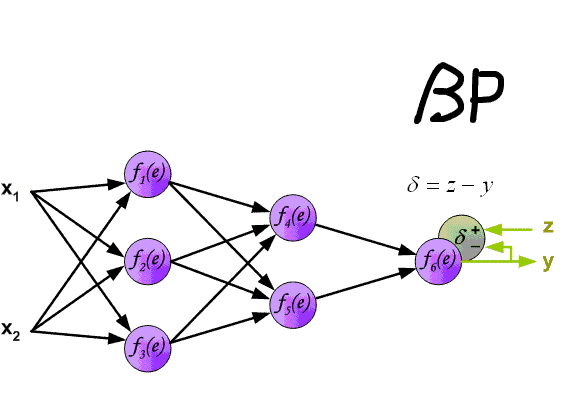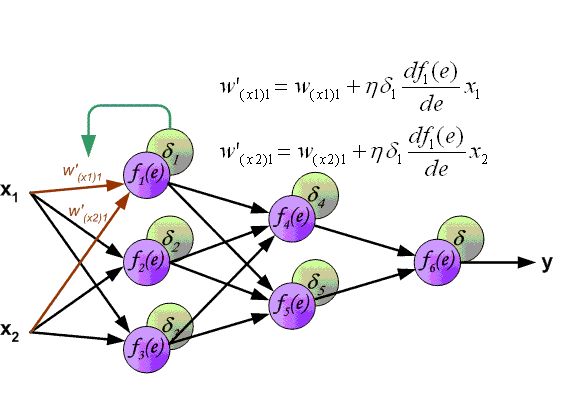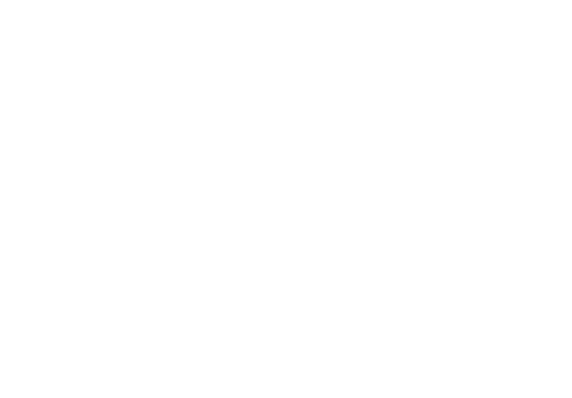
L'essence de cette méthode est que, sur la base de la valeur obtenue de scaled_loss et de la matrice des poids du modèle trainable_weights, les dérivées des poids du modèle sont calculées de gauche à droite, sur l'ensemble du graphique de calcul. C'est-à-dire que l'on prend la valeur de la fonction de perte scaled_loss et que l'on trouve les dérivées pour les valeurs obtenues à la sortie du décor, puis pour les valeurs obtenues dans l'encodeur, et ainsi de suite jusqu'aux valeurs initiales du modèle. L'objectif est de trouver la valeur des dérivées de manière à minimiser la fonction de perte. D'un point de vue conceptuel, le schéma d'apprentissage du réseau neuronal souhaité ressemble à ceci: la fonction de perte prend une valeur minimale → nous trouvons les poids correspondant à cette valeur → l'erreur est minimale → la prédiction du réseau neuronal est précise. Visuellement, le schéma de calcul du vecteur de gradient et le mécanisme de rétropropagation peuvent être représentés comme suit.
(Image 11 - calcul du vecteur de gradient)
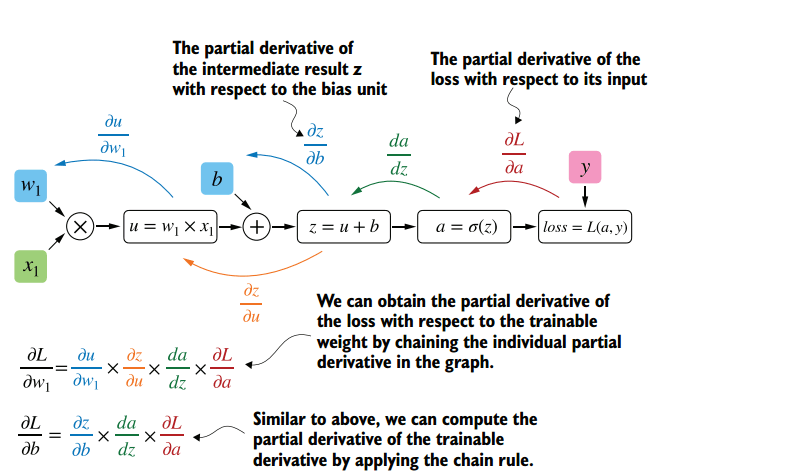
(Image 12 - mécanisme de rétropropagation)
- lors de l'entraînement avec une précision mixte (FP16), les gradients sont divisés par la valeur loss_scale à l'aide de la fonction optimizer optimizer.get_unscaled_gradients(gradients) ; ci-dessous se trouve une tranche des poids du modèle et de ses gradients (début et fin de la matrice) ; (Image 13 - tranche des poids du modèle et de ses gradients)

- Ainsi, nous obtenons une matrice de gradients dont la taille est équivalente à celle de la matrice des poids du modèle. Par exemple, si le modèle contient 1 million de paramètres, la matrice de gradients contiendra également 1 million de valeurs.
- Après avoir calculé la matrice de gradients pour tous les groupes (lots), les gradients sont accumulés. Par exemple, pour une taille de lot efficace de 200 000 et une taille de lot de 6 250, le nombre de groupes sera de 32. Autrement dit, après le calcul des gradients, nous aurons 32 matrices de gradients (chaque lot ayant sa propre matrice de gradients). Ces gradients sont accumulés en additionnant les matrices entre elles. En plus de l'accumulation des matrices de gradients, les valeurs obtenues dans les fonctions loss et loss_token_normalizer (nombre total de tokens cibles dans le lot) sont également accumulées pour former les variables suivantes:
━ loss = all_reduce_sum(loss)
━ sample_size = all_reduce_sum(loss_token_normalizer)
- Après l'accumulation des matrices de gradients, de loss et de loss_token_normalizer, la valeur des gradients est divisée par le nombre total de tokens dans le groupe ( sample_size ). Par exemple, ci-dessous, le mécanisme est illustré pour trois lots contenant un total de 146 tokens. (Image 14 - mécanisme des trois lots).

- À l'aide de la fonction apply_gradients de la classe optimiseur, les gradients sont appliqués aux poids du modèle, c'est-à-dire que les poids du modèle sont mis à jour. Mise en œuvre du mécanisme de mise à jour des poids de l'optimiseur d'Adam. L'algorithme de mise à jour des poids en utilisant une valeur de notre exemple:
━ momentsum et velocities - sont initialement initialisés à zéro. Elles contiennent les valeurs de momentum pour chaque poids du modèle et seront ajustées et mises à jour à chaque étape ;
━ alpha - valeur adaptative du paramètre du taux d'apprentissage.
(Image 15 - application des gradients aux poids du modèle)
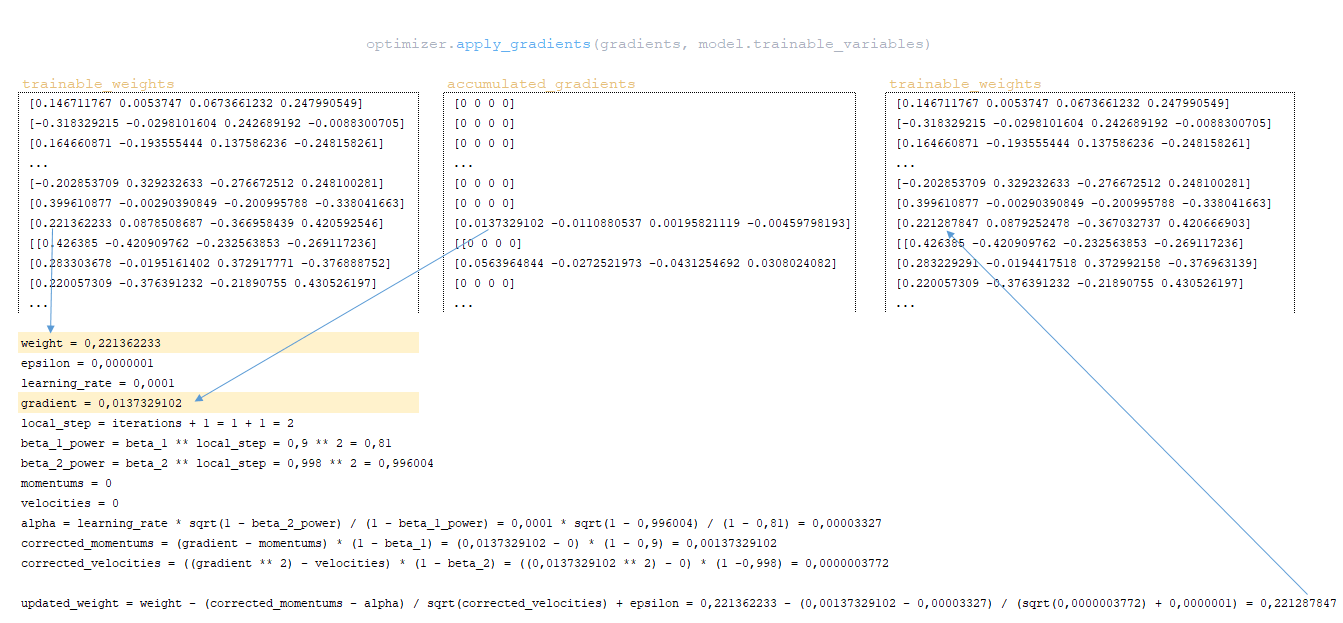
Lors de l'utilisation d'un autre type d'optimiseur, le mécanisme de calcul et d'application des gradients sera différent.
Séquence d’appels simplifiée:
├── def call() class Trainer, module training.py
├── def _steps() class Trainer, module training.py
├── def _accumulate_gradients(batch) class Trainer, module training.py
├── def compute_gradients() class Model(tf.keras.layers.Layer), module model.py
├── def _accumulate_loss() class Trainer, module training.py
├── def call() class GradientAccumulator, module optimizers/utils.py
├── def _apply_gradientss() class Trainer, module training.py
Après l’application des gradients, la valeur de la fonction de perte est divisée par le nombre total de tokens:
loss = float(loss) / float(sample_size) → 40.6409149 / 12 = 3.38674291.
Cette valeur est affichée dans le journal d’entraînement: Step = 1; Loss = 3.386743. Elle est également utilisée pour tracer le graphique de la fonction de perte d’entraînement affiché dans Tensorboard.
Conclusion
L'article conclut en mettant en lumière les processus critiques impliqués dans le calcul des pertes et l'application des gradients dans les modèles d'apprentissage automatique. En comprenant comment ces composants interagissent, notamment les ajustements pour l'alignement et le calcul précis des gradients, les chercheurs peuvent optimiser leurs modèles pour améliorer leur précision et leurs performances.