Το άρθρο εξηγεί τον τρόπο λειτουργίας του κωδικοποιητή σε ένα νευρωνικό δίκτυο, περιγράφοντας λεπτομερώς τα βήματα που εμπλέκονται στην προετοιμασία των δεδομένων και τον υπολογισμό των παραστάσεων συμβόλων. Ξεκινά με την αρχικοποίηση του συνόλου δεδομένων και περιγράφει τον κύκλο εκπαίδευσης, συμπεριλαμβανομένου του τρόπου με τον οποίο τα δεδομένα ομαδοποιούνται σε παρτίδες για επεξεργασία.
Οι βασικές διαδικασίες όπως η ενσωμάτωση, η εγκατάλειψη, η ομαλοποίηση και ο μηχανισμός προσοχής συζητούνται, εστιάζοντας στους ρόλους των διαφόρων εξαρτημάτων όπως η SelfAttentionencoderlayer και η Layernorm. Το άρθρο καλύπτει επίσης τους γραμμικούς μετασχηματισμούς και τη χρήση της σχετικής κωδικοποίησης θέσης, εξηγώντας τον τρόπο με τον οποίο τα δεδομένα εισόδου μετατρέπονται μέσω πολλαπλών στρωμάτων πριν αποσταλούν στον αποκωδικοποιητή. Συνολικά, παρέχει πλήρη κατανόηση της λειτουργικότητας του κωδικοποιητή και τη σημασία του στα μοντέλα κατάρτισης.
Έναρξη λειτουργίας κωδικοποιητή
Μετά την αρχικοποίηση, λαμβάνουν χώρα τα ακόλουθα βήματα:
- Το σύνολο δεδομένων ολοκληρώνεται, δηλ. Το Ολόκληρο Ενεργοποιείται ο αγωγός προετοιμασίας δεδομένων κατάρτισης.
├ .. Ομάδες εξάγονται από το σύνολο δεδομένων κατάρτισης που ομαδοποιούνται σε παρτίδες.
├ .. call () | κλάση WordEmbedder (TextInputter) Μονάδα text_inputter.py
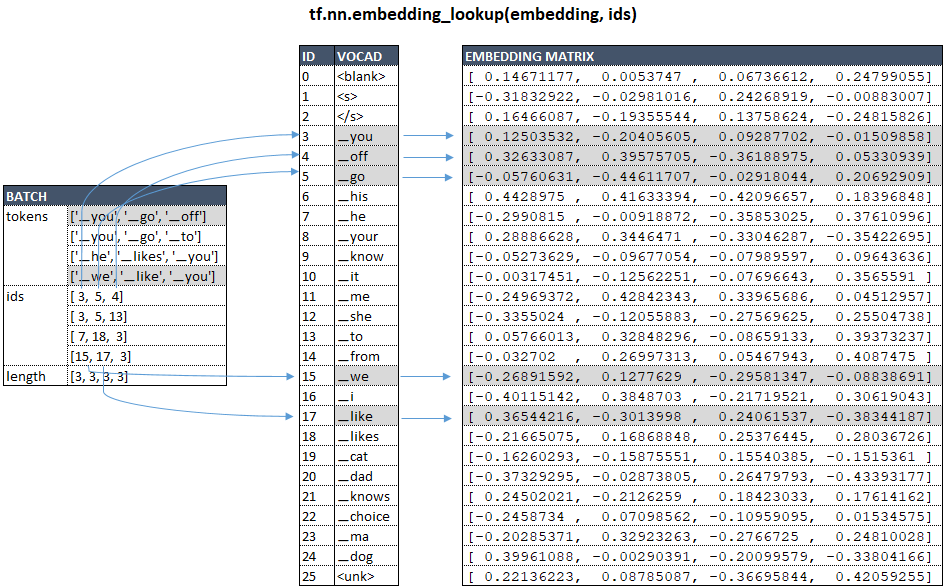
Χρησιμοποιώντας το παράδειγμα του μοντέλου μας με vocab_size = 26 και num_units = 4 , σχηματικά, για Πηγή Γλώσσα αυτό μπορεί να αντιπροσωπεύεται ως εξής: (Εικόνα 1 - Matrix ενσωμάτωσης)
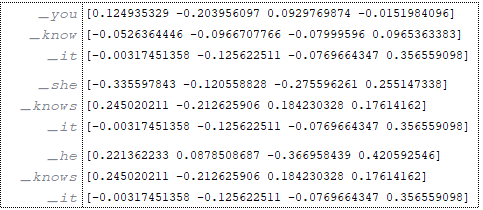
Ας υποθέσουμε ότι οι παρτίδες μας αποτελούνται από 3 στοιχεία κατάρτισης.
Πηγή: (Εικόνα 2 - Πηγή)
στόχος: (εικόνα 3 - στόχος)
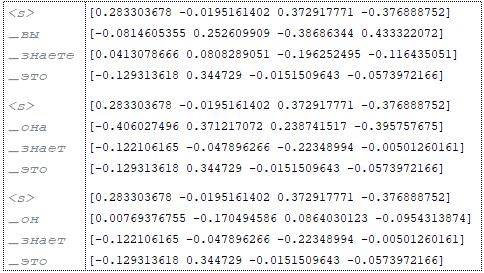
Στο προετοιμασία φορέα κωδικοποιητή των Tokenes Πηγή Γλώσσα :
- πολλαπλασιάζεται με την τετραγωνική ρίζα της διάστασης - εισόδους = εισόδους * √ (Εικόνα 4 - num_units = 4)
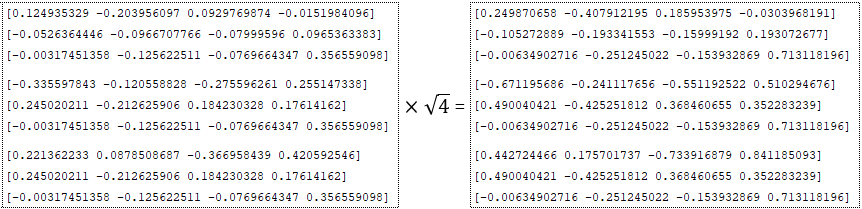
- Η απόρριψη εφαρμόζεται ( παράσταση από το αρχείο διαμόρφωσης), δηλ. Οι τιμές αντικαθίστανται τυχαία από το μηδέν χρησιμοποιώντας τη συνάρτηση tf.nn.dropout . Ταυτόχρονα, όλες οι άλλες τιμές (εκτός από εκείνες που αντικαταστάθηκαν από το μηδέν) ρυθμίζονται με πολλαπλασιασμό με 1/(1 - p) , όπου p είναι η πιθανότητα εγκατάλειψης. Αυτό γίνεται για να φέρει τις τιμές στην ίδια κλίμακα, η οποία επιτρέπει τη χρήση του ίδιου δικτύου για εκπαίδευση (σε πιθανότητα <1 (Εικόνα (σε ,0) - 5 < li Παράμετρος εγκατάλειψης) και πιθανότητα=1,0). συμπεράσματα>

- Με τη διάσταση των παρτίδων, το tf.equence_mask Η λειτουργία του mask tensor; Για το παράδειγμα μας, η διαστάσεις των παρτίδων θα είναι [3 3 3] και η συνάρτηση επιστρέφει τη μάσκα. (Εικόνα 6 - TF.Sequence_mask)
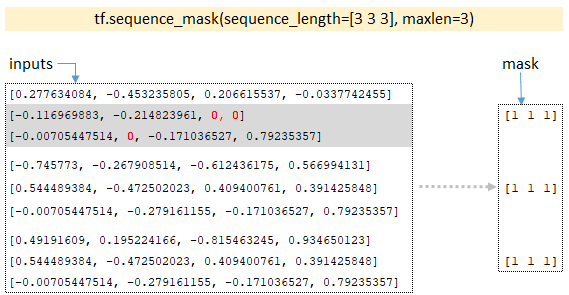
- Στον βρόχο, για κάθε στρώμα , ίσο με τον αριθμό των παραμέτρων , η διανυσματική αναπαράσταση του διανυσματικού φορέα (που αποθηκεύεται στο μεταβλητό εισόδους ) και η μάσκα μεταφέρεται στο στρώμα , το αποτέλεσμα που επιστρέφεται με το layer στρώμα . Για παράδειγμα, εάν έχουμε 6 στρώματα, το αποτέλεσμα από το πρώτο στρώμα θα είναι το αποτέλεσμα εισόδου για το δεύτερο στρώμα, κλπ.

- Κάθε στρώμα αντιπροσωπεύει ένα αντικείμενο της κατηγορίας selfAttentionEncoderlayer , στην οποία ο μηχανισμός προσοχής εφαρμόζεται χρησιμοποιώντας την κλάση . Ο μηχανισμός των μετασχηματισμών που εμφανίζονται σε κάθε στρώμα selfAttentionEncoderlayer περιγράφεται παρακάτω.
Στρώμα κανονικοποίησης, κλάση layernorm ()
Με την παράμετρο pre norm = true , εφαρμόζεται ένα στρώμα κανονικοποίησης στην παρτίδα μετά από dropout και τη λειτουργία κάλυψης, πριν από τον υπολογισμό των βαρών προσοχής - για κάθε απορροή παρτίδας με k υπολογίζουμε τον μέσο όρο και τη διακύμανση:
mean_i = άθροισμα (x_i [j] για j στην περιοχή (k))/k
var_i = άθροισμα ((x_i [j] - mean_i) ** 2 για j στην περιοχή (k))/k
Στη συνέχεια, υπολογίζεται η κανονικοποιημένη τιμή x_i_normalized , συμπεριλαμβανομένου ενός μικρού παράγοντα Epsilon (0,001) για αριθμητική σταθερότητα, υπολογίζεται:
x_i_normalized = (x_i - mean_i) / sqrt (var_i + epsilon) v < / b>
Και τέλος, x_i_normalized μετασχηματίζεται γραμμικά χρησιμοποιώντας το γάμμα και το βήτα, οι οποίες είναι εκπαιδευτικές παράμετροι (κατά την αρχικοποίηση gamma = [1, ..., 1], beta = [0, ..., 0] ):
output_i = x_i_normalized * gamma + betaoutput_i = x_i_normalized * gamma + beta
Οι τιμές των ερωτημάτων
Γραμμικός μετασχηματισμός, κλάση πυκνό ()
━ 1) Η διάσταση των παρτίδων υπολογίζεται → shape = [3, 3, 4] ;
━ 2) Αλλάζει τη διαστάσεων tf.reshape tf.reshape (εισόδους, [-1, 4]) ; (Εικόνα 7 - tf.reshape)

━ 3) με mixed_precision και num_units διαιρούνται κατά 8, το μέγεθος της επένδυσης και ο σχηματισμός του υπολογίζεται
padding_size = 8 - num_units % 8 → padding_size = 8 - 4 % 8 = 4
paddings = [[0, 0], [0, padding_size]] → Paddings = [[0, 0], [0, 4]]
Τα βάρη του στρώματος kernel (τα οποία σχηματίστηκαν κατά την αρχικοποίηση) των ερωτημάτων href = 'https://www.tensorflow.org/api_docs/python/tf/pad'> tf.pad (πυρήνας, paddings) ; (Εικόνα 8 - tf.pad)

━ 4) Οι πίνακες href = 'https://www.tensorflow.org/api_docs/python/tf/linalg/matmul'> tf.matmul (εισόδους, πυρήνας) πολλαπλασιάζονται. (Εικόνα 9 - tf.matmul)

━ 5) Μια φέτα της διάστασης στρώματος num_units λαμβάνεται από τη μήτρα που προκύπτει και το outputs σχηματίζεται. (Εικόνα 10 - Έξοδος Matrix)

━ 6) Ο φορέας bias προστίθεται στον πίνακα outputs που λαμβάνεται στο προηγούμενο βήμα (αρχικά bias Οι τιμές αρχικοποιούνται με το στρώμα kernel και αρχικά είναι ίσες με το μηδέν) href = 'https://www.tensorflow.org/api_docs/python/tf/nn/bias_add'> tf.nn.bias_add (εξόδους, προκατάληψη) ; (Εικόνα 11 - tf.nn.bias_add)
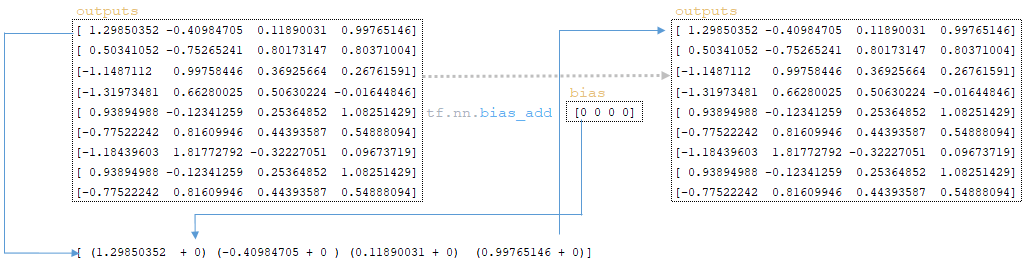
━ 7) Μετά την προσθήκη Bias , η Matrix έξοδοι υφίσταται ενεργοποίηση γραμμικής στρώσης (έξοδοι). Η γραμμική ενεργοποίηση στρώματος είναι η εφαρμογή μιας συνάρτησης στη μήτρα. Δεδομένου ότι η συνάρτηση για το στρώμα tf.keras.layers.dense δεν ορίζεται, από προεπιλογή, η λειτουργία ενεργοποίησης είναι a (x) = x , δηλαδή η μήτρα παραμένει αμετάβλητη. (Εικόνα 12 - ενεργοποίηση)
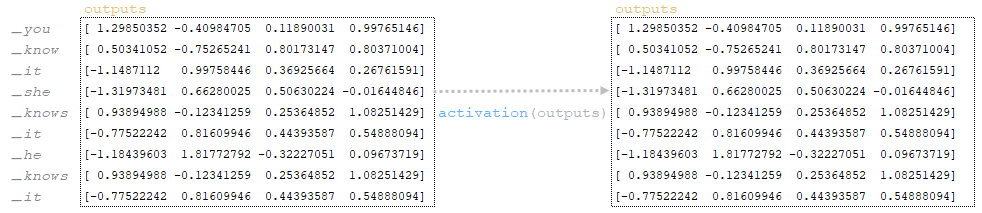
━ 8) Μετά την ενεργοποίηση του γραμμικού στρώματος, η μήτρα αναδιαμορφώνεται tf.reshape (εξόδους, σχήμα [:-1] + [num_units]) → tf.reshape Μετά από αυτό το βήμα παίρνουμε τα ερωτήματα . (Εικόνα 13 - Matrix Queries)

Τα ερωτήματα που λαμβάνεται στο προηγούμενο βήμα διαιρείται από τον αριθμό των κεφαλών (στην αρχιτεκτονική μας ο αριθμός των κεφαλών είναι 2, ο μηχανισμός της διαίρεσης περιγράφεται στο πρώτο μέρος του άρθρου). (Εικόνα 14 - Έρωτα Matrix διαιρούμενο με τον αριθμό των κεφαλών)
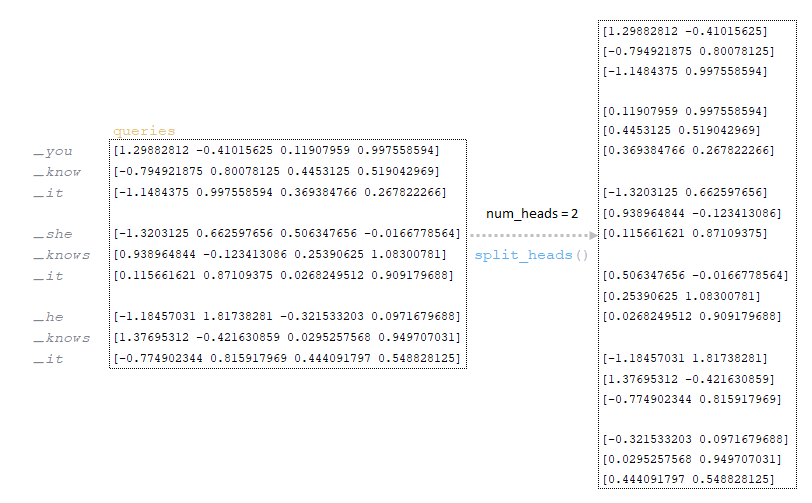
Διαιρούμενο με τον αριθμό των κεφαλών Τα ερωτήματα διαιρείται με την τετραγωνική ρίζα: (Εικόνα 15 - Ερωτήσεις μήτρας διαιρούμενο με τετραγωνική ρίζα)

num_units_per_head:
num_units_per_head = num_units // num_heads
num_units_per_head = 4 // 2 = 2
Σύμφωνα με τα βήματα 1-8 που περιγράφηκαν παραπάνω (στοιχείο γραμμικού μετασχηματισμού), ο πίνακας υπολογίζεται και διαιρείται με τον αριθμό των γκολ. (Εικόνα 16 - Κλειδιά Matrix)

Μετά τα βήματα 1-8 παραπάνω, οι τιμές υπολογίζονται και διαιρούνται με τον αριθμό των στόχων. (Εικόνα 17 - Τιμές μήτρας)

Σχετική κωδικοποίηση
Δεδομένου ότι το εξεταζόμενο παράδειγμα χρησιμοποιεί σχετική θέση κωδικοποίησης (maximum_relative_position = 8) , το επόμενο βήμα είναι η σχετική κωδικοποίηση:
━ 1) Η διάσταση του πίνακα υπολογίζεται:
keys_length = tf.shape (πλήκτρα) [2]
keys_length = [3 2 3 2 2] [2]
keys_length = 3;
━ 2) σχηματίζεται μια σειρά ακέραιων στοιχείων μήκους keys_length :
arange = tf.Range (μήκος)
arange = [0 1 2];
━ 3) Δύο μήτρες στον άξονα 0 και 1 σχηματίζονται χρησιμοποιώντας τη συνάρτηση απόσταση = tf.expand_dims (arange, 0) - tf.expand_dims (arange, 1) ; (Εικόνα 18 - Matrix Distance)
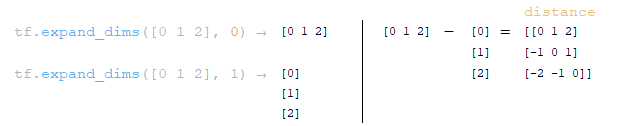
━ 4) Η απόσταση από την απόσταση απόσταση διαγώνια είναι κομμένη στην τιμή του maximum_relative_position tf.clip_by_value (απόσταση, -maximum_position, maximum_position) ; (Εικόνα 19 - Maximpy_relative_position)
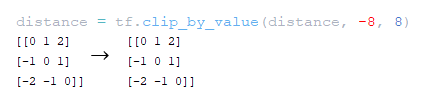
━ 5) Η τιμή του maximum_relative_position προστίθεται στην απόσταση απόσταση που λαμβάνεται στο προηγούμενο βήμα. (Εικόνα 20 - απόσταση + mater_position matrix)
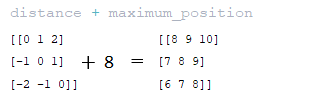
━ 6) Ο πίνακας relative_pos που λαμβάνεται στο προηγούμενο βήμα χρησιμοποιείται για την εξαγωγή από το relative_position_keys matrix που σχηματίζεται στο μοντέλο αρχικοποίησης. (Εικόνα 21 - relative_repr_keys matrix)
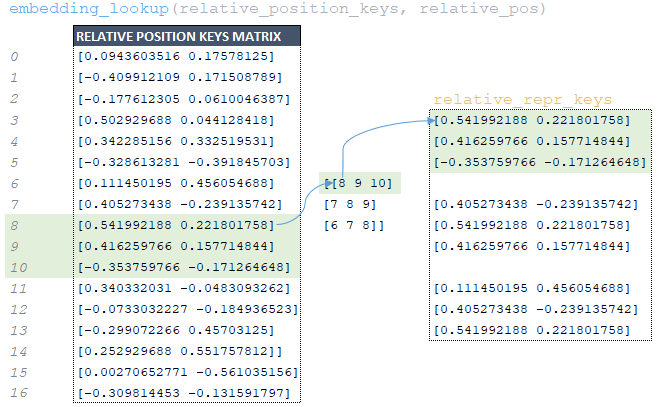
━ 7) Το Matrix relative_repr_values → ombedding_lookup (relative_position_values, relative_pos) σχηματίζεται με τον ίδιο τρόπο. (Image 22 - relative_repr_values matrix)
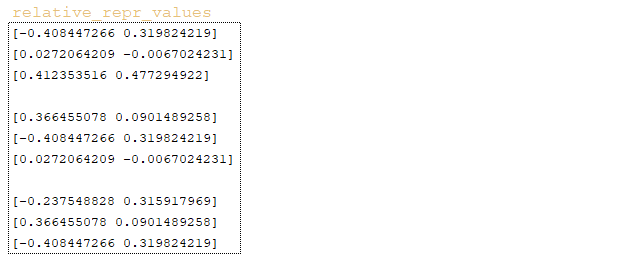
Κλιμακωτό προϊόν
Το επόμενο βήμα είναι το κλιμακωτό προϊόν των ερωτημάτων Matrix (Εικόνα 23 - Σκικευμένο προϊόν ερωτημάτων και πλήκτρων)
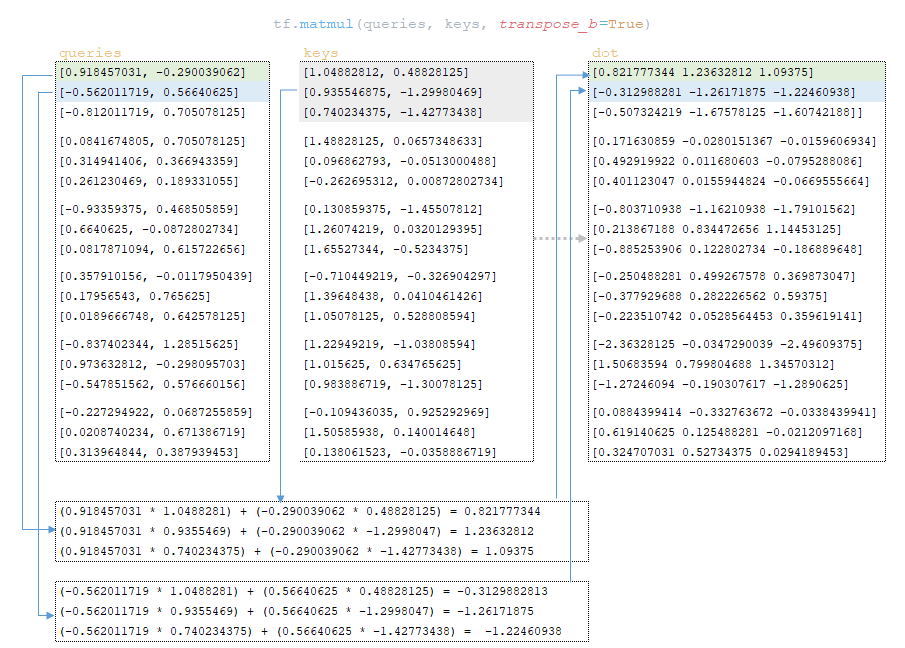
Τα ερωτήματα πολλαπλασιάζονται με το matrix relative_repr_keys → matmul_with_relative_representations (ερωτήματα, relative_repr_keys, transpose_b = true) . (Image 24 - Matrix Queries πολλαπλασιασμένο με matrix relative_repr_keys)
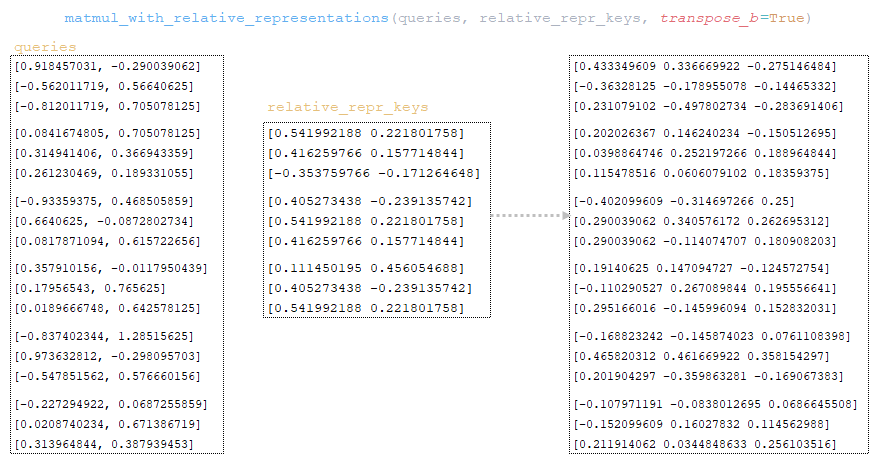
Στη μήτρα dot προστίθεται η μήτρα που λαμβάνεται στο βήμα matmul_with_relative_representations . (Εικόνα 25 - Dot Matrix)

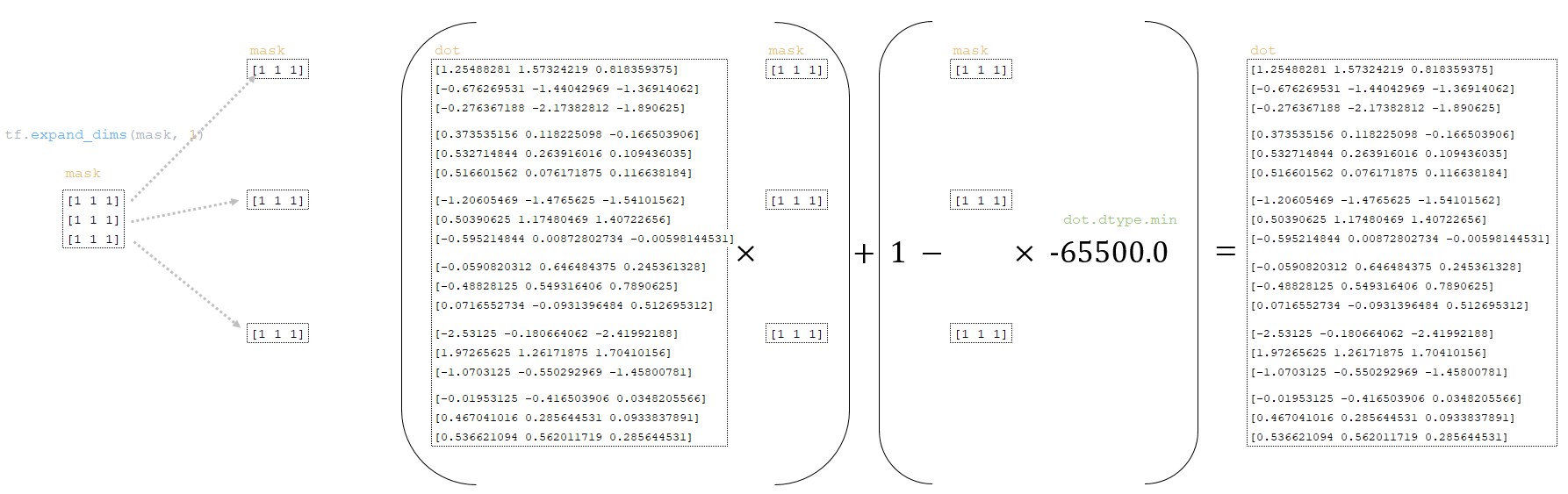
Η μήτρα dot μετασχηματίζεται χρησιμοποιώντας τη μάσκα που λαμβάνεται από τις παρτίδες συμβολικών προβολών παραπάνω:
━ 1) Η διάσταση της μάσκας μάσκας αλλάζει μάσκα = tf.expand_dims (μάσκα, 1)
━ 2) Το dot Η μήτρα dot μετατρέπεται ως εξής
dot = (dot * mask) + (1.0 - μάσκα) * dot.dtype.min
(Εικόνα 26 - μήτρες κουκίδων και μάσκας)
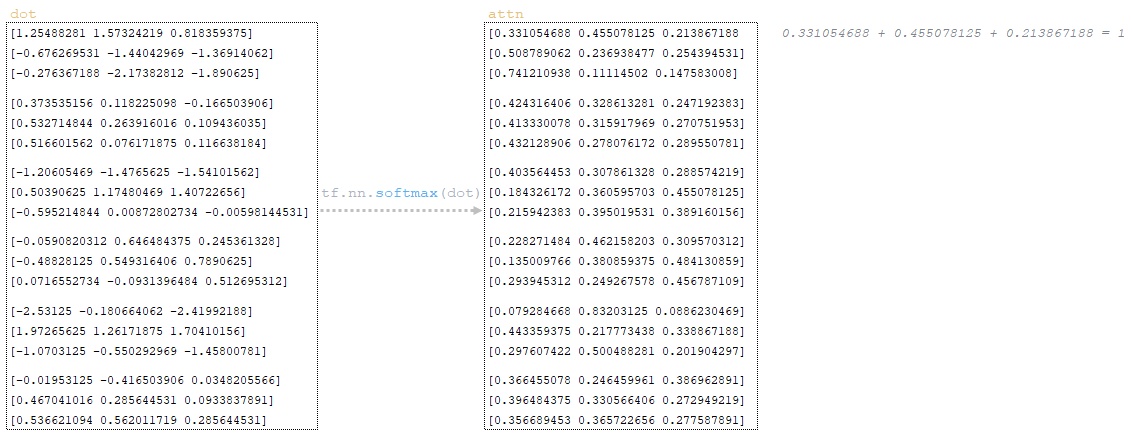
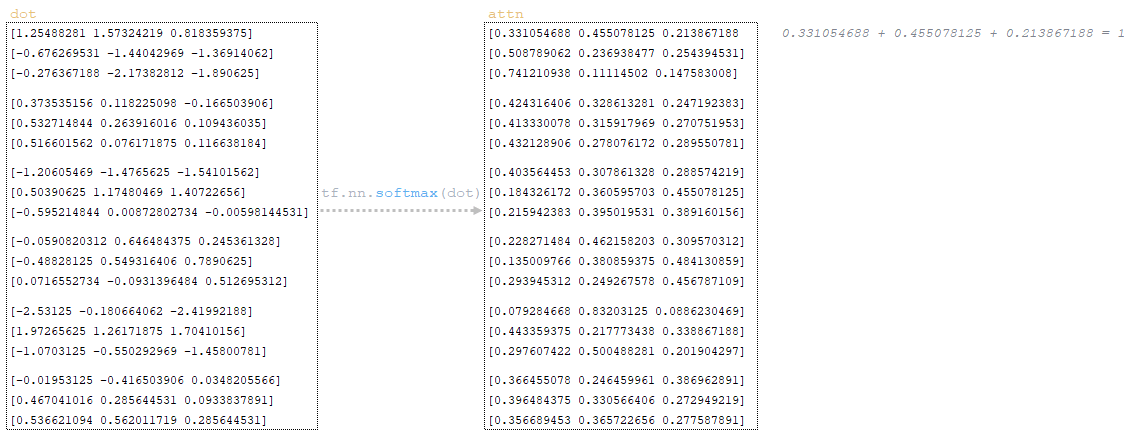
Η λειτουργία ενεργοποίησης softmax εφαρμόζεται στη μήτρα dot και λαμβάνουμε το matrix attn → attn = tf.nn.softmax (dot) . Η λειτουργία softmax χρησιμοποιείται για να μετατρέψει τον φορέα των τιμών σε κατανομή πιθανότητας που συνοψίζει έως 1. (Εικόνα 27 - Εφαρμογή SoftMax)
Dropout εφαρμόζεται στη μήτρα attn (παράμετρος προσοχή_dropout από το αρχείο διαμόρφωσης). (Εικόνα 28 - Εφαρμογή εγκατάλειψης)
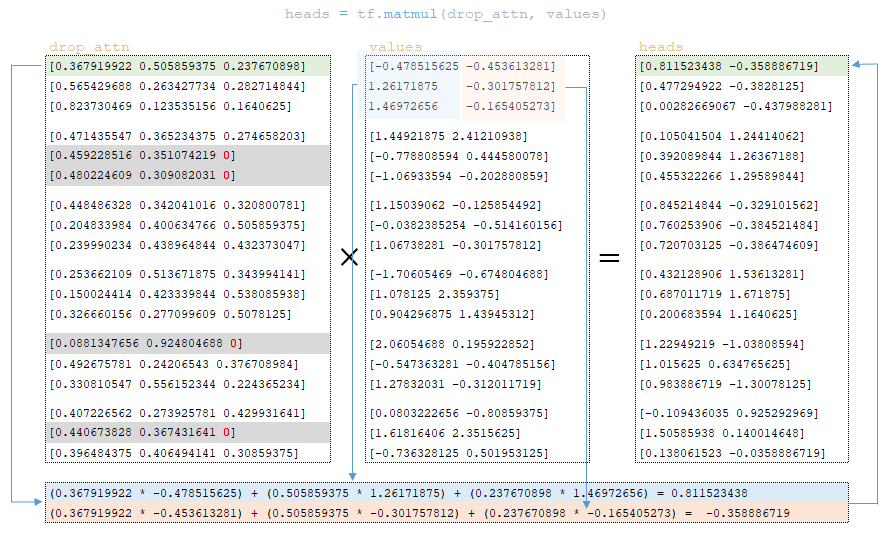
Μετά την εγκατάλειψη, η μήτρα drop_attn πολλαπλασιάζεται με τις τιμές για να σχηματίσουν τις κεφαλές . (Εικόνα 29 - κεφαλές μήτρας)
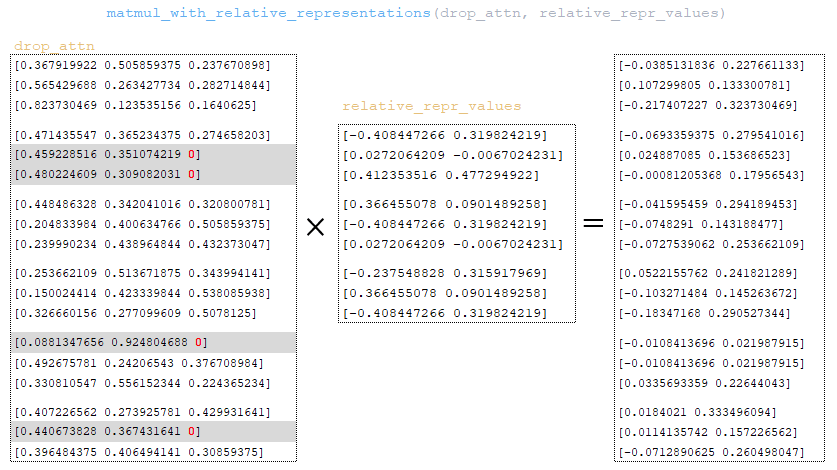
Η μήτρα drop_attn πολλαπλασιάζεται με το matrix relative_repr_values . (Εικόνα 30 -drop_attn matrix)
Η μήτρα που λαμβάνεται στο matmul_with_relative_representations προστίθεται στις κεφαλές matrix. (Εικόνα 31 - Matrix Heads)

Οι κεφαλές κεφαλές μετατρέπονται στη διάσταση της αρχικής παρτίδας μέσω του tf.nn.relu
━ 3) dropout εφαρμόζεται (παράμετρος ffn_dropout από το αρχείο διαμόρφωσης)
━ 4) Γραμμικός μετασχηματισμός πυκνής () κλάσης
━ 5) dropout εφαρμόζεται (παράμετρος dropout από το αρχείο διαμόρφωσης)
━ 6) Εφαρμοσμένος υπολειπόμενος σύνδεσμος
(Εικόνα 36- Μεταφορά της μήτρας εξόδων για να τροφοδοτήσει το δίκτυο προς τα εμπρός)
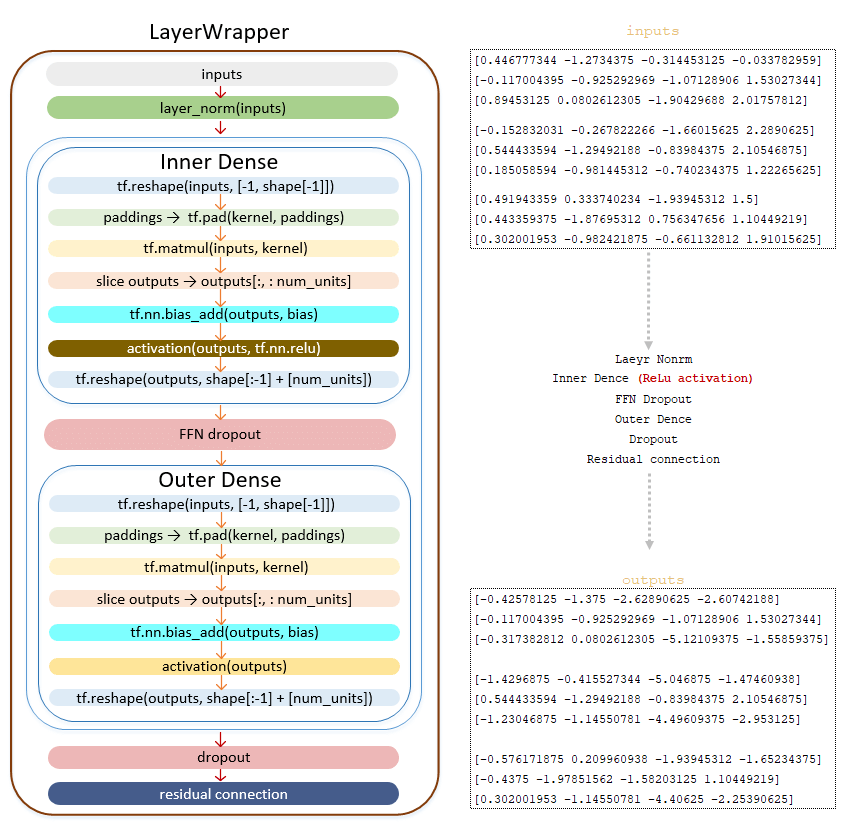
Εάν η τιμή των στρώσεων είναι μεγαλύτερη από μία, τότε μετά τη μετατροπή των εξόδων χρησιμοποιώντας το δίκτυο feed forward, η προκύπτουσα μήτρα αποστέλλεται στην είσοδο του επόμενου στρώματος μέχρι να περάσει από όλα τα στρώματα.
Λήψη Matrix Έξοδοι από το τελευταίο στρώμα , περνάει το στρώμα κανονικοποίησης layernorm () - την τελική λειτουργία στον κωδικοποιητή. Η μήτρα που λαμβάνεται σε αυτό το βήμα μεταβιβάζεται στον αποκωδικοποιητή. (Εικόνα 37 - Layer Normalization LayerNorm ())
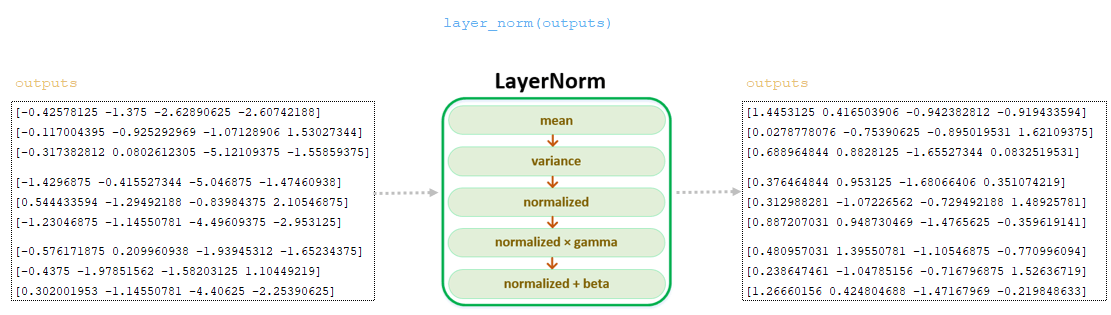
Ο προαναφερθέντος μηχανισμός μετατροπής της Πηγής των παρτίδων συμβόλων γλώσσας στον κωδικοποιητή μπορούν να χαρτογραφηθούν ως εξής. (Εικόνα 38 - Μηχανισμός για τη μετατροπή του Tokenization της γλώσσας προέλευσης στον κωδικοποιητή)
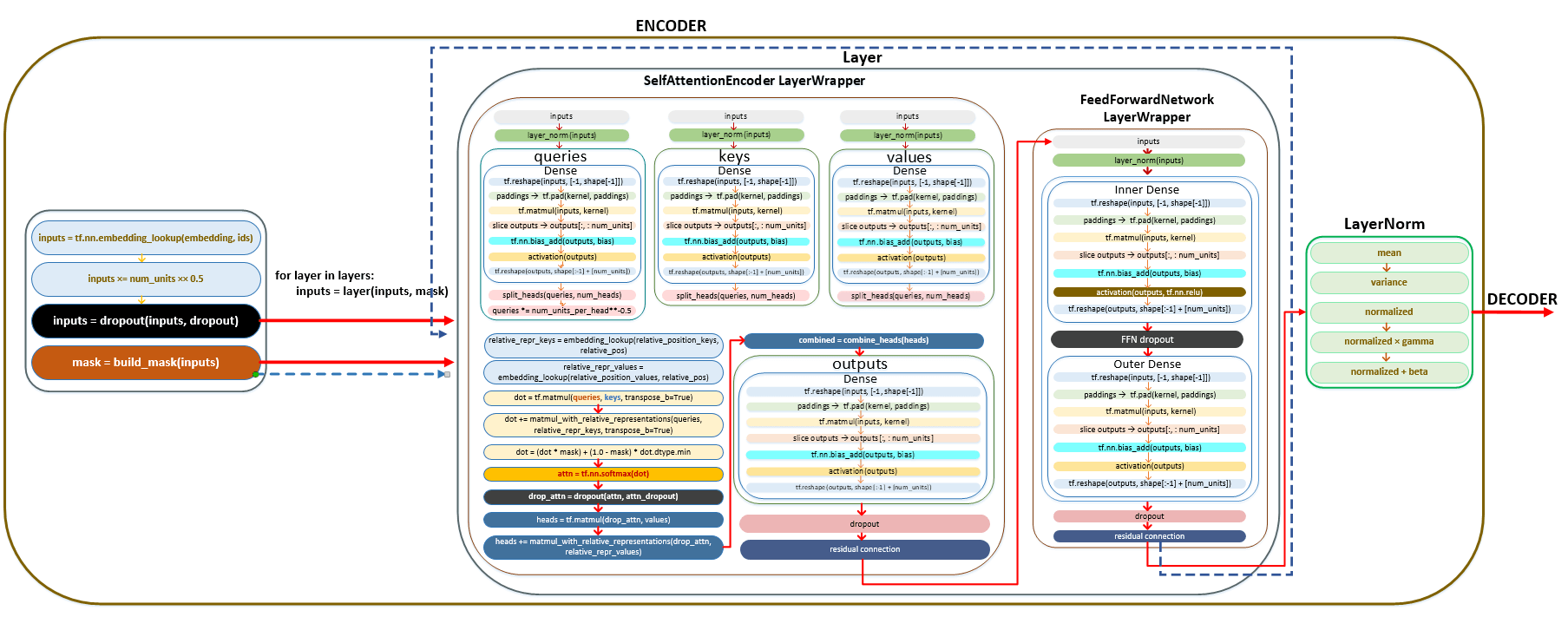
κωδικοποιητής. Απλοποιημένη ακολουθία κλήσεων:
├ .. Μοντέλο κλάσης (tf.keras.layers.layer) module model.py
├ .. def call () | Κατηγορία SequenceTosequence (Model.SequenceGenerator) Μονάδα sequence_to_sease.py
├ .. def call () | κλάση WordEmbedder (TextInputter) Μονάδα text_inputter.py
├ .. def () | Class SelfAttentionEncoder (κωδικοποιητής) Μονάδα self_attention_encoder.py
├ .. def def () | Class SelfAttentionencoderlayer (tf.keras.layers.layer) Μονάδα layers/transformer.py
├ .. def call () | Κατηγορία Multiheadattention (tf.keras.layers.layer) Μονάδα Layers/Transformer.py
├ .. def call () | Κατηγορία feedforwardnetwork (tf.keras.layers.layer) Μονάδα layers/transformer.py
├ ..
Τελικά, η έξοδος του κωδικοποιητή επεξεργάζεται περαιτέρω μέσω της ομαλοποίησης και ενός δικτύου τροφοδοσίας, με υπολειμματικές συνδέσεις που εξασφαλίζουν αποτελεσματική κατάρτιση. Στη συνέχεια παρασκευάζεται η τελική έξοδος του κωδικοποιητή για τον αποκωδικοποιητή, που απεικονίζει τον κρίσιμο ρόλο του κωδικοποιητή στη μετατροπή των σημείων εισόδου σε σημαντικές αναπαραστάσεις για την επακόλουθη επεξεργασία.
↑× - Κάθε στρώμα αντιπροσωπεύει ένα αντικείμενο της κατηγορίας selfAttentionEncoderlayer , στην οποία ο μηχανισμός προσοχής εφαρμόζεται χρησιμοποιώντας την κλάση . Ο μηχανισμός των μετασχηματισμών που εμφανίζονται σε κάθε στρώμα selfAttentionEncoderlayer περιγράφεται παρακάτω.