Αυτό το άρθρο ασχολείται με αρκετές προηγμένες τεχνικές που αποσκοπούν στη βελτίωση της αποτελεσματικότητας και της αποτελεσματικότητας της κατάρτισης. Θα συζητήσουμε μεθόδους που βοηθούν στη σταδιακή προσαρμογή των παραμέτρων μοντέλου, οι οποίες μπορούν να οδηγήσουν σε πιο σταθερές μαθησιακές διαδικασίες. Με την τελειοποίηση του τρόπου και όταν τα βάρη μοντέλων ενημερώνονται, αυτές οι τεχνικές αποσκοπούν στην ενίσχυση της σύγκλισης και τελικά να αποδώσουν καλύτερα αποτελέσματα.
Επιπλέον, το άρθρο θα καλύψει στρατηγικές για τη διαχείριση των ποσοστών μάθησης, τα οποία διαδραματίζουν κεντρικό ρόλο στον προσδιορισμό του πόσο γρήγορα μαθαίνει ένα μοντέλο. Η κατανόηση του τρόπου προσαρμογής αυτών των ποσοστών με την πάροδο του χρόνου μπορεί να επηρεάσει σημαντικά τη δυναμική της κατάρτισης και να οδηγήσει σε ταχύτερα και πιο ακριβή μοντέλα.
Τέλος, θα διερευνήσουμε τη σημασία της διαχείρισης σημείων ελέγχου, η οποία επιτρέπει την καλύτερη αξιοποίηση των εκπαιδευμένων μοντέλων με τον μέσο όρο βάρους από πολλαπλές εκπαιδευτικές συνεδρίες. Αυτό μπορεί να βοηθήσει στην άμβλυνση των επιπτώσεων της υπερφόρτωσης και στη διασφάλιση ότι το μοντέλο διατηρεί τα καλύτερα χαρακτηριστικά που έχουν μάθει κατά τη διάρκεια του ταξιδιού του κατάρτισης.
Εκθετικός κινητός μέσος όρος
Στο προεπιλεγμένο αρχείο διαμόρφωσης του μοντέλου μετασχηματιστή, η παράμετρος moving_average_decay δεν έχει οριστεί. Έχοντας ορίσει την παράμετρο moving_average_decay σε μια τιμή κοντά σε μία (σύμφωνα με το Η μετακίνηση είναι αρχική.
- Ο συντελεστής decay υπολογίζεται: decay = 1 - min (0.9999, (1.0 + training_step)/(10.0 + training_step))
- Ο ακόλουθος αλγόριθμος εφαρμόζεται σε κάθε βάρος μοντέλου: shadow_weigth = προηγούμενο_weight - (προηγούμενο_weight - current_weight) * decay
- Τα εξομαλυνθείσα βάρη μετά από κάθε βήμα εκπαίδευσης αποθηκεύονται στην κλάση movingaverage . Η αντικατάσταση των εκπαιδευμένων βαρών με εξομαλυνθείσα βάρη συμβαίνει μόνο όταν αποθηκεύεται το σημείο ελέγχου του μοντέλου. (Εικόνα 1 - ExponentialMovingAverage)

Απλοποιημένη ακολουθία κλήσεων:
├ .. call () Εκπαιδευτής κλάσης module truct.py
├ .. init () Κλάση MovingAverage Μονάδα training.py
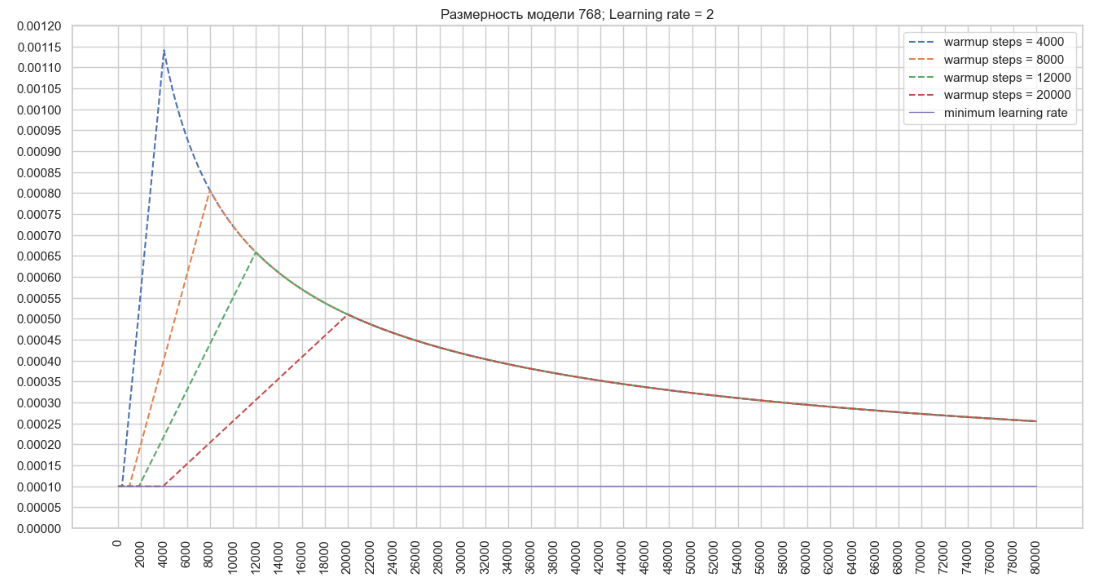
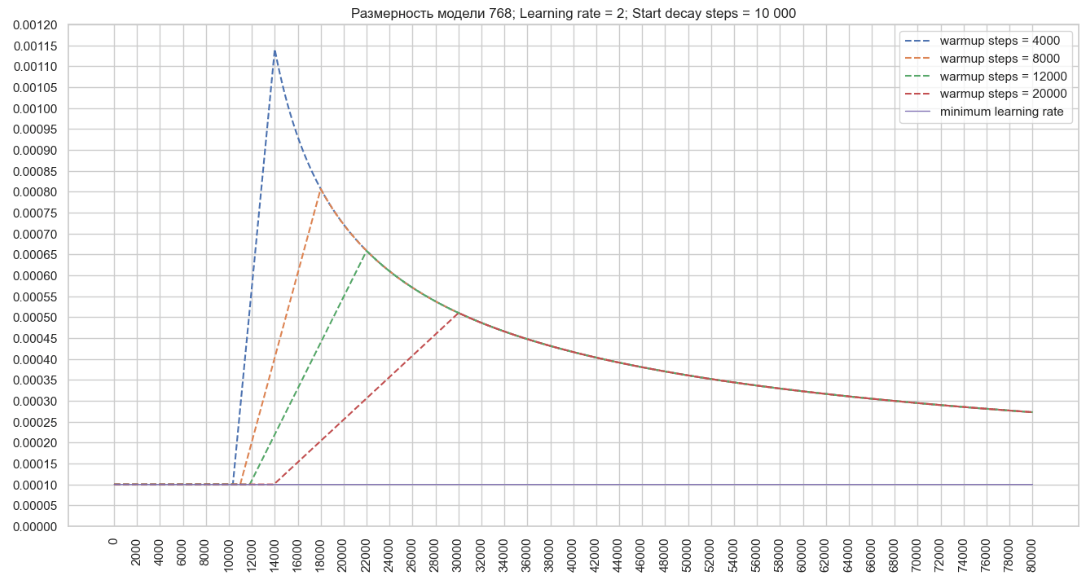
├ .. Μονάδα training.py Ο μηχανισμός αποσύνθεσης χρησιμοποιεί μεταβλητές που αρχικοποιούνται στις κατηγορίες noamdecay και schedulewrapper . Μετά από κάθε βήμα κατάρτισης, εμφανίζονται οι ακόλουθοι μετασχηματισμοί στην κλάση ScheduleWrapper: Στην κλάση noamdecay εμφανίζονται οι ακόλουθοι μετασχηματισμοί: Στην κλάση schedulewrapper , ορίζεται η τελική τιμή του συντελεστή: rate -rate = tf.maximum (learning_rate, inximply_learning_rate) → ρυθμός εκμάθησης = max (0,000002795, 0,0001) = 0,000002795 = 0,0001 . Αυτή είναι η τιμή που εξέρχεται στο αρχείο καταγραφής εκπαίδευσης: βήμα = 1; Ποσοστό μάθησης = 0,000100; Απώλεια = 3.386743 . Χρησιμοποιώντας τον αλγόριθμο που περιγράφηκε παραπάνω, θα σχεδιάσουμε ένα γράφημα αλλαγών στο ποσοστό μάθησης του βελτιστοποιητή για ένα μοντέλο με διάσταση 768 και την καθορισμένη παράμετρο ρυθμό μάθησης = 2 στο αρχείο διαμόρφωσης εκπαιδευτή. (Εικόνα 2 - Ποσοστό μάθησης = 2) Τώρα ας σχεδιάσουμε ένα γράφημα αλλαγών στην τιμή μάθησης Από τα γραφήματα, μπορούμε να καταλήξουμε στο συμπέρασμα ότι με τη μείωση της τιμής του του βέλτιστου του βελτιστοποιητή που μπορεί να συμβάλει γρήγορα με την αύξηση του ρυθμού μάθησης στο config, είναι δυνατόν να επιτευχθούν υψηλότερες τιμές του ποσοστού μάθησης του βελτιστοποιητή που μπορεί να συμβάλει στην ταχύτερη εκμάθηση με μια μεγάλη διαμόρφωση μοντέλου. Μπορείτε επίσης να επηρεάσετε τη μεταβολή του ρυθμού εκμάθησης χρησιμοποιώντας την παράμετρο start_decay_steps , δηλαδή μπορούμε να καθορίσουμε πόσα βήματα θα εφαρμοστούν μετά την έναρξη της κατάρτισης του μηχανισμού warmup_steps και της επακόλουθης αποσύνθεσης. Το παρακάτω γράφημα δείχνει ότι με start_decay_steps = 10.000 , τα πρώτα 10 χιλιάδες βήματα το μοντέλο εκπαιδεύεται με σταθερό ρυθμό μάθησηςΜηχανισμός αποσύνθεσης ποσοστού εκμάθησης
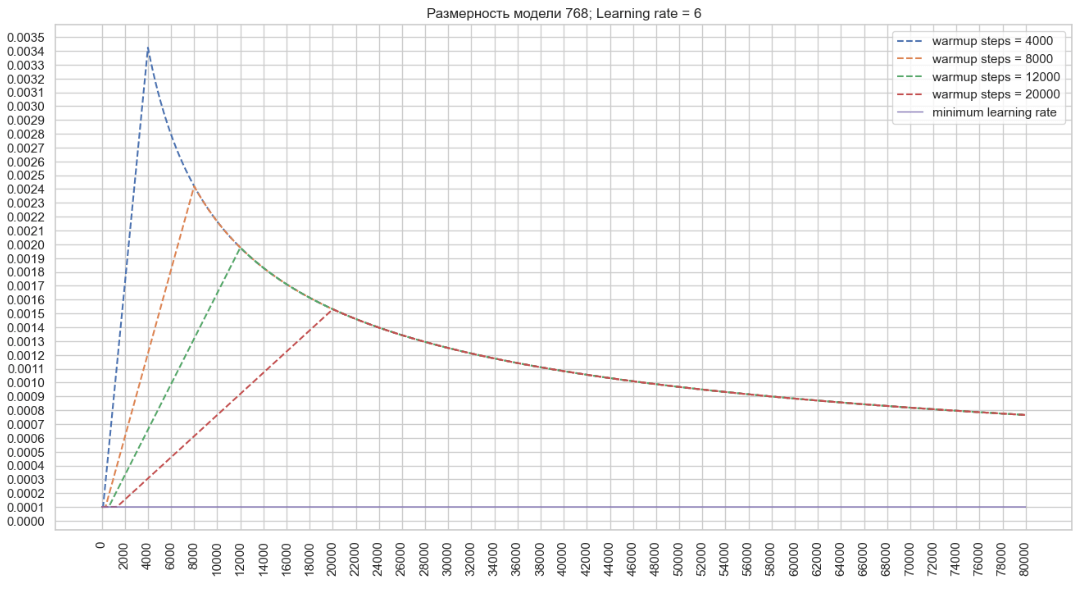
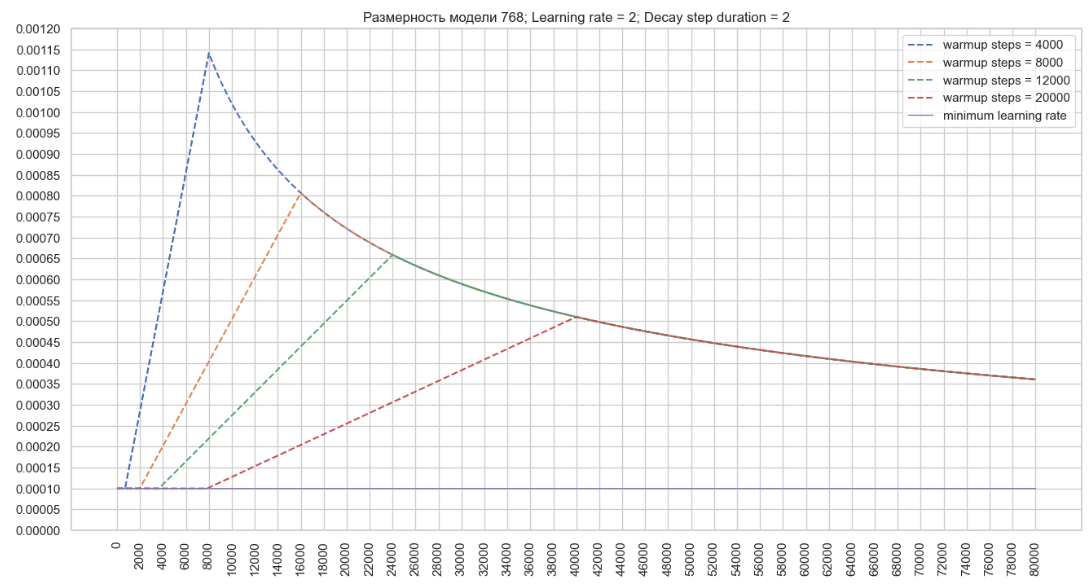
Η παράμετρος decay_step_duration μπορεί να χρησιμοποιηθεί για να αυξήσει τη διάρκεια του μηχανισμού warmup_steps και να επιβραδύνει τον ρυθμό αποσύνθεσης. (Εικόνα 5 - decay_step_duration)
Απλοποιημένη ακολουθία κλήσεων:
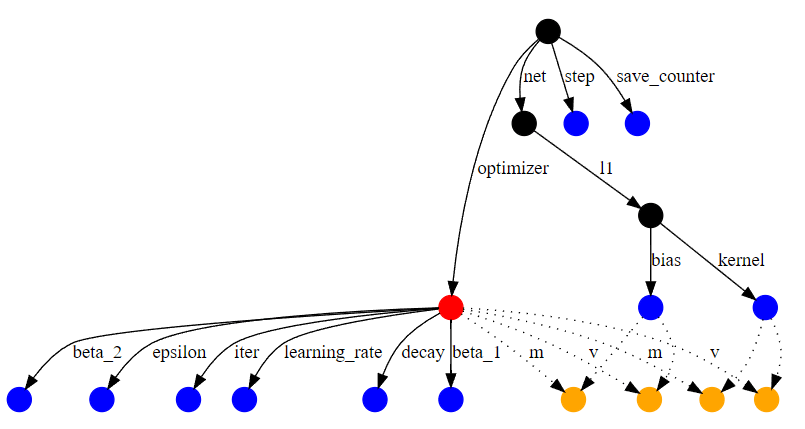
├ .. Μονάδα Προγράμματα/lr_schedules.py ├ .. Noamdecay Μονάδα Προγράμματα/lr_schedules.py ├ .. Μονάδα Προγράμματα/lr_schedules.py Ένα σημείο ελέγχου είναι μια κατάσταση μοντέλου σε ένα συγκεκριμένο βήμα κατάρτισης. Ένα εκπαιδευμένο σημείο ελέγχου μοντέλου αποθηκεύει τα βάρη μοντέλου που άλλαξε κατά τη διάρκεια της εκπαίδευσης, τις μεταβλητές βελτιστοποιητή για κάθε στρώμα (την κατάσταση βελτιστοποιητή σε ένα συγκεκριμένο βήμα κατάρτισης) και ένα γράφημα υπολογισμού. Ένα παράδειγμα ενός μικρού γραφήματος υπολογισμού για ένα απλό δίκτυο εμφανίζεται στον αριθμό εικόνας 6 - το γράφημα υπολογισμού. (Εικόνα 6 - Το γράφημα υπολογισμού) Ο βελτιστοποιητής επισημαίνεται με κόκκινες, κανονικές μεταβλητές είναι μπλε και οι μεταβλητές υποδοχής βελτιστοποίησης είναι πορτοκαλί. Άλλοι κόμβοι επισημαίνονται με μαύρο χρώμα. Οι μεταβλητές υποδοχής αποτελούν μέρος της κατάστασης βελτιστοποίησης, αλλά δημιουργούνται για μια συγκεκριμένη μεταβλητή. Για παράδειγμα, οι παραπάνω άκρες «M» αντιστοιχούν στη δυναμική ότι τα κομμάτια Adam Optimizer για κάθε μεταβλητή. Στο τέλος της εκπαίδευσης, τα σημεία ελέγχου του μοντέλου διαβάζονται από τον κατάλογο μοντέλων και αποκαθίστανται σε μια ποσότητα ίση με την παράμετρο exion_last_checkpoints . Σύμφωνα με την αρχιτεκτονική του εκπαιδευμένου μοντέλου, τα βάρη αρχικοποιούνται με τιμή μηδέν για όλα τα στρώματα του μοντέλου. Στη συνέχεια στο βρόχο, για κάθε ανακαινισμένο σημείο ελέγχου, τα βάρη διαβάζονται. Τα βάρη κάθε στρώματος διαιρούνται από τον αριθμό των σημείων ελέγχου που καθορίζονται στην παράμετρο μέσης_χρυσωτή_checkpoints και οι προκύπτουσες τιμές προστίθενται στα βάρη που αρχικοποιήθηκαν παραπάνω χρησιμοποιώντας το Λειτουργία (το στρώμα ενσωμάτωσης αθροίζεται μόνο με το στρώμα ενσωμάτωσης κλπ.) Ο μέσος μηχανισμός ενός μικρού στρώματος από το μοντέλο παραδείγματος, με τον μέσο όρο των δύο τελευταίων σημείων ελέγχου, εμφανίζεται στην εικόνα 7. Συμπερασματικά, οι τεχνικές που συζητούνται σε αυτό το άρθρο προσφέρουν πολύτιμες γνώσεις για τη βελτιστοποίηση της κατάρτισης μοντέλων βαθιάς μάθησης. Με την εφαρμογή στρατηγικών για την προσαρμογή του βάρους, τη διαχείριση του ποσοστού μάθησης και τον μέσο όρο των σημείων ελέγχου, οι επαγγελματίες μπορούν να ενισχύσουν σημαντικά την απόδοση και τη σταθερότητα του μοντέλου. Αυτές οι μέθοδοι όχι μόνο διευκολύνουν τις ομαλότερες διαδικασίες κατάρτισης αλλά και βοηθούν στην επίτευξη καλύτερης σύγκλισης και γενίκευσης. Τελικά, με την κατανόηση και την εφαρμογή αυτών των εννοιών, οι ερευνητές μπορούν να βελτιώσουν τις ροές εργασίας τους, οδηγώντας σε πιο αποτελεσματικές και αποτελεσματικές λύσεις μηχανικής μάθησης.Μηχανισμός μέσου όρου ελέγχου

Σύναψη
↑