Το άρθρο παρέχει μια ολοκληρωμένη επισκόπηση του υπολογισμού της συνάρτησης απώλειας στη μηχανική μάθηση, ιδιαίτερα στο πλαίσιο των μοντέλων αλληλουχίας. Ξεκινά με λεπτομερώς τον τρόπο με τον οποίο η Matrix Logits, που δημιουργείται μετά από μετασχηματισμούς στον αποκωδικοποιητή, επεξεργάζεται μέσω της συνάρτησης Cross_Entropy_Sequence_loss. Αυτή η συνάρτηση διαδραματίζει κρίσιμο ρόλο στη μέτρηση της απόκλισης μεταξύ των προβλεπόμενων εξόδων και των πραγματικών ετικετών. Τα εμπλεκόμενα βήματα περιλαμβάνουν τη μετατροπή των logits σε μια κατάλληλη μορφή, την εφαρμογή της εξομάλυνσης της ετικέτας για τη δημιουργία ομαλοποιημένων ετικετών και τον υπολογισμό της απώλειας διασταυρούμενης εντροπίας χρησιμοποιώντας το SoftMax. Κάθε μετασχηματισμός εξηγείται σχολαστικά, καθιστώντας σαφές πώς κάθε στοιχείο συμβάλλει στη συνολική αξιολόγηση των ζημιών.
Εκτός από τον υπολογισμό των ζημιών, το άρθρο εξετάζει τον μηχανισμό ευθυγράμμισης που χρησιμοποιείται για την ενίσχυση της απόδοσης του μοντέλου. Περιγράφει τον τρόπο με τον οποίο η τιμή απώλειας ρυθμίζεται με βάση την καθοδηγούμενη ευθυγράμμιση, επιτρέποντας στο μοντέλο να υπολογίζει καλύτερα τις σχέσεις μεταξύ προέλευσης και προορισμών ακολουθιών. Η διαδικασία υπολογισμού και εφαρμογής των κλίσεων είναι επίσης λεπτομερής, που απεικονίζει τον τρόπο με τον οποίο το βελτιστοποιητή ενημερώνει τα βάρη μοντέλων για την ελαχιστοποίηση της απώλειας.

Υπολογισμός συνάρτησης απώλειας
Η διαδικασία ξεκινά με τη μήτρα logits που λαμβάνεται μετά από μετασχηματισμούς στον αποκωδικοποιητή και η παρτίδα γλωσσικής γλωσσών μεταδίδεται στο cross_entropy_rosecence_loss Λειτουργία. (Εικόνα 1 - Matrix Logits)

Οι ακόλουθες μετασχηματισμοί πραγματοποιούνται μέσα στη λειτουργία:
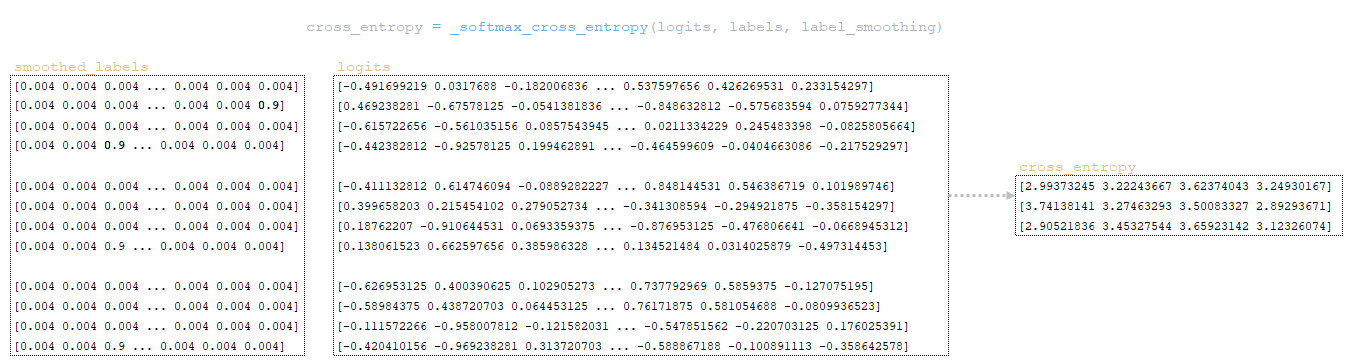
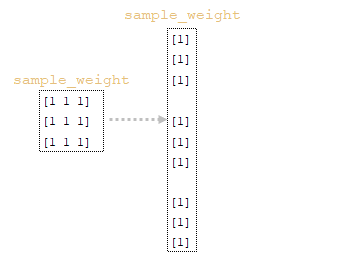
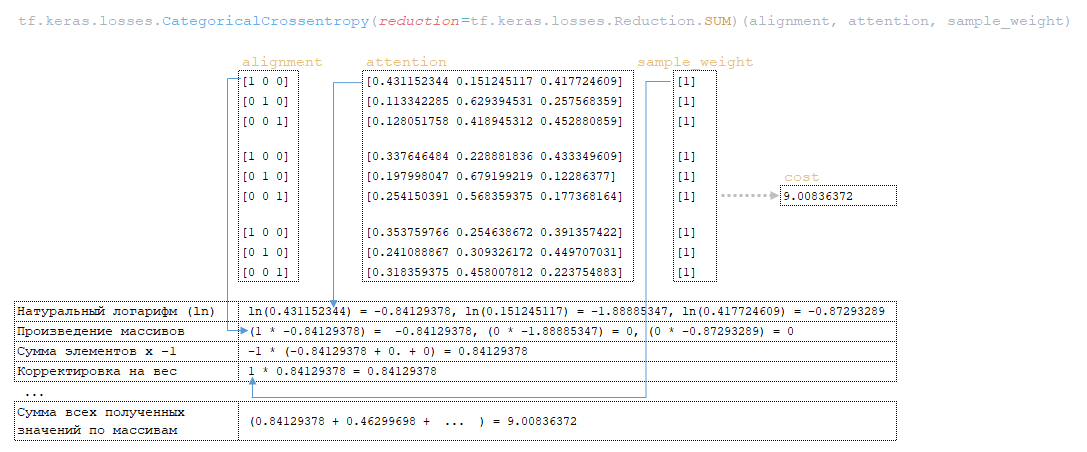
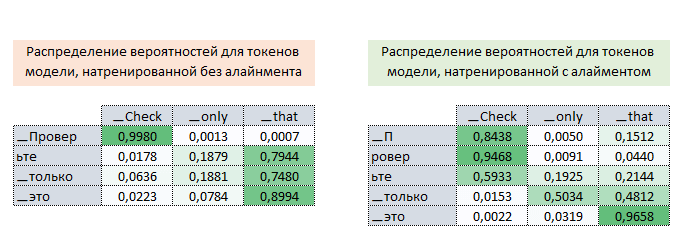
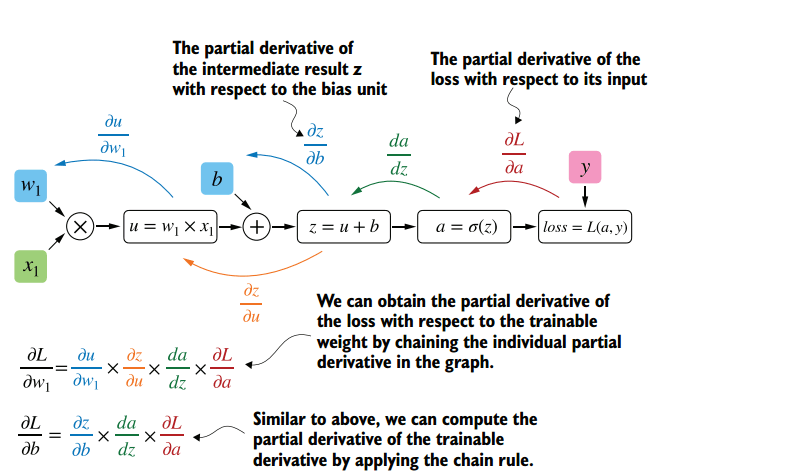
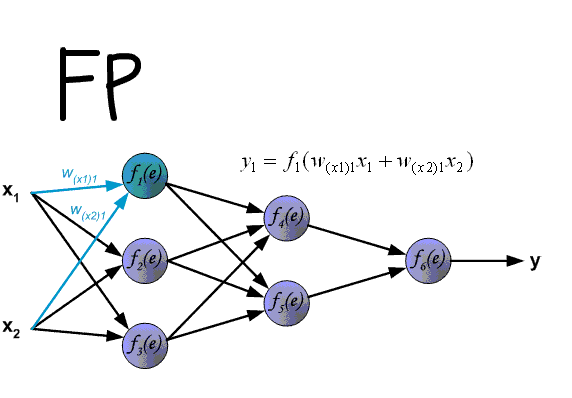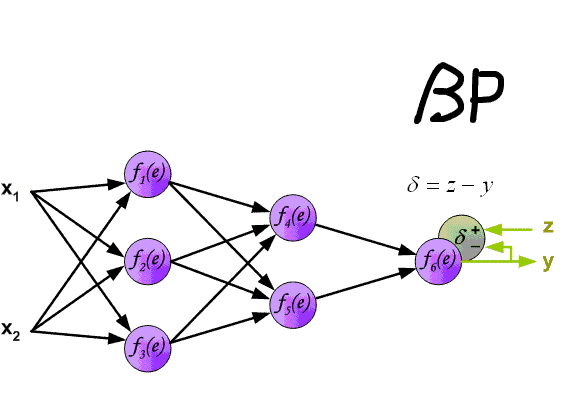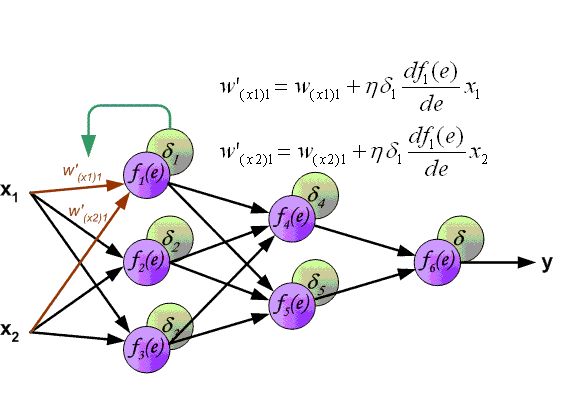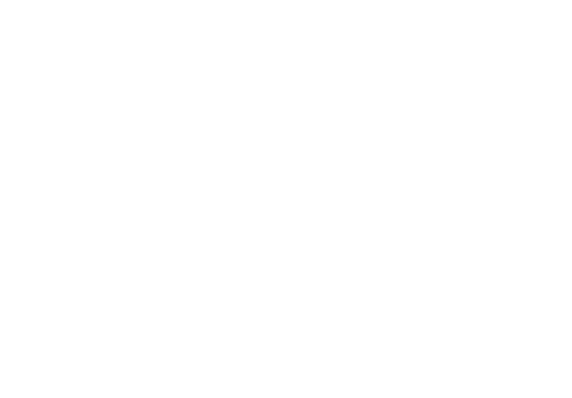
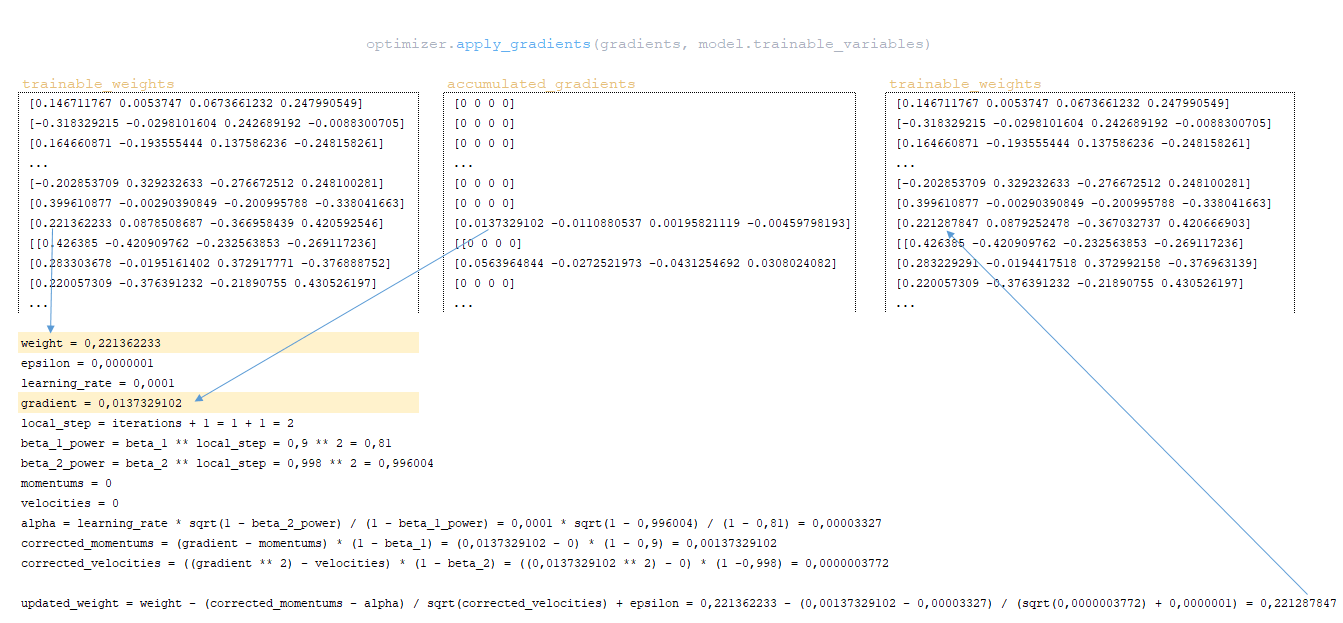
Η μήτρα Cross_Entropy υπολογίζεται χρησιμοποιώντας το Ο αλγόριθμος για αυτή τη λειτουργία έχει ως εξής: - Ο εκθέτης του logits υπολογίζεται - ισοδύναμα numpy.exp (logits); - Τα στοιχεία της μήτρας συνοψίζονται στη γραμμή ανά γραμμή - ισοδύναμα με το numpy.sum (numpy.exp (logits), axis = -1). - Ο δεκαδικός λογάριθμος της ληφθέντης μήτρας λαμβάνεται και μεταφέρεται από τη διάσταση του logits (3, 1, 1). - Η μήτρα που λαμβάνεται στο προηγούμενο βήμα αφαιρείται από το matrix για να σχηματίσει το logsoftmax matrix → logsoftmax = logits - numpy.log (numpy.sum (numpy.exp (logits), axis = -1)). 1) ; - Cross_Entropy θεωρείται - το logsoftmax matrix πολλαπλασιάζεται με το αρνητικό logits matrix και το προϊόν συνοψίζεται γραμμή με γραμμή → cross_entropy = numpy.sum (logsoftMax * -labels, axis = -1) (Εικόνα 3 - Cross_Entropy) 2) Χρησιμοποιώντας τη συνάρτηση tf.reishence_mask (Αυτή η μεταβλητή περιέχει τις τιμές των μήκους προτάσεων σε μάρκες που ομαδοποιούνται σε μια παρτίδα) και τη διαστασιότητα της μήτρας logits.shape [1] [3, 4, 26]. (Εικόνα 4 - βάρος) 3) Χρησιμοποιώντας τη συνάρτηση tf.math.reduce_sum ) = 39.6399841 από το προϊόν των πινάκων cross_entropy και βάρος ; (Εικόνα 5 - Προϊόν Cross_Entropy και Weight Matrices) 4) Χρησιμοποιώντας τη συνάρτηση tf.math.reduce_sum Το varible loss_token_normalizer βάρος , το οποίο θα είναι ίσο με τον αριθμό των μαρκών στη μάχη → loss_token_normalizer = tf.reduce_sum (βάρος) = 12 ; 5) Το αποτέλεσμα επιστρέφει δύο μεταβλητές απώλεια = 39.6399841 και loss_token_normalizer = 12 . Απλοποιημένη ακολουθία κλήσεων: ├ .. module truct.py ├ .. Ενότητα model.py ├ .. module model.py ├ .. Μονάδα sequence_to_sequence.py ├ .. def cross_entropy_lossence () utils/losses.py Κατά την κατάρτιση ενός μοντέλου με ευθυγράμμιση, η τιμή στη μεταβλητή , που λαμβάνεται στο προηγούμενο βήμα, προσαρμόζεται χρησιμοποιώντας το guided_alignment_cost ferembercost . Οι ακόλουθες μετασχηματισμοί πραγματοποιούνται μέσα στη λειτουργία: 1) Ανάλογα με τον τύπο ευθυγράμμισης καθοδηγούμενου τύπου στο αρχείο διαμόρφωσης, καθορίζεται η λειτουργία μετατροπής: - Για ce τιμή - tf.keras.losses.categoricalcrossentropy (μείωση = tf.keras.losses.reduction.sum) - Για την τιμή MSE - tf.keras.losses.meansquarederror 2) Η διάρκεια των προτάσεων σε μάρκες υπολογίζεται από το στόχο γλωσσικές παρτίδες. (Εικόνα 6 - get_length) 3) Χρησιμοποιώντας τη συνάρτηση tf.equence_mask χρησιμοποιώντας τα ληφθέντα μήκη και τη διάσταση του πίνακα προσοχή tf.shape (προσοχή) [1]. Για το παράδειγμα μας, η διάρκεια των προτάσεων σε μάρκες θα είναι [3 3 3 3] και η διάσταση της μήτρας προσοχή [3 3 3 3]. (Εικόνα 7 - δείγμα_weight) 4) με τη συνάρτηση tf.expand_dims (input, axis) Το δείγμα δείγμα δείγμα δείγμα sample_powe/b> είναι επαναληπτικό = tf.expand_dims (sample_weight, -1) ; (Εικόνα 8 - Τροποποιημένη μήτρα δειγματοληψίας) 5) Χρησιμοποιώντας τη συνάρτηση TF.Reduce_sum, ο κανονικοποιητής → Normalizer = TF.Reduce_sum ([3 3 3 3]) = 9 υπολογίζεται από τη σειρά των μήκους των προτάσεων. 6) Χρησιμοποιώντας τη συνάρτηση tf.keras.losses.CategoricalCrossentropy (ευθυγράμμιση, προσοχή) , η τιμή του κόστους cost υπολογίζεται χρησιμοποιώντας το Matrix (το τελευταίο στοιχείο προσοχή [:, -1] Σε κάθε διάνυσμα της διανυσματικής αναπαράστασης του διακριτικού στο πλέγμα έχει αφαιρεθεί εκ των προτέρων, έτσι ώστε οι διαστάσεις της μήτρας να συμπίπτουν, επειδή η διάσταση της αρχικής μήτρας είναι η προσοχή . (Εικόνα 9 - Υπολογισμός μεταβλητής τιμής κόστους) 7) Η μεταβλητή κόστος < / b> διαιρείται με τη μεταβλητή normalizer → κόστος = κόστος / κανονικοποιητή = 9.00836372 / 9 = 1.00092936 < / b>. 8) Μεταβλητή Το κόστος πολλαπλασιάζεται με την τιμή της μεταβλητής βάρος (παράμετρο από το αρχείο διαμόρφωσης Βάρος ευθυγράμμισης καθοδηγούμενου ) → κόστος = βάρος * βάρος = 1.00092936 * 1 = 1.00092936 . 9) Η τιμή από τη μεταβλητή που λαμβάνεται στη συνάρτηση cross_entropy_equence_loss διορθώνεται με την τιμή της μεταβλητής . Απλοποιημένη ακολουθία κλήσεων: ├ .. module truct.py ├ .. Ενότητα model.py ├ .. module model.py ├ .. Μονάδα sequence_to_sequence.py ├ .. def guided_alignment_cost () Έτσι, επαναλαμβανόμενες, κατά τη διαδικασία εκπαίδευσης του μοντέλου με ευθυγράμμιση, προσαρμόζουμε την αξία της συνάρτησης απώλειας (αυξάνοντας την αξία του) και επομένως "αναγκάζει" τον βελτιστοποιητή για να ελαχιστοποιηθεί η συνάρτηση απώλειας λαμβάνοντας υπόψη την επίδραση της ευθυγράμμισης. Η παρακάτω εικόνα δείχνει τις κατανομές πιθανοτήτων των πινάκων των σημάτων γλωσσών των σημείων γλωσσών των πλήρως εκπαιδευμένων μοντέλων χωρίς και με ευθυγράμμιση. Οι κατανομές δείχνουν ότι με τις πιθανότητες του Matrix των μοντέλων με ευθυγράμμιση των σημάτων [п, р р р р р р р р р р р р р р р р р р р р р р р р р р р р р р р р р р р р р р р р ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь ь (Εικόνα 10 - μήτρα με και χωρίς ευθυγράμμιση) Η διαδικασία υπολογισμού και εφαρμογής κλίσης έχει ως εξής: Η ουσία αυτής της μεθόδου είναι αυτή που βασίζεται στην ληφθείσα τιμή scaled_loss και στον πίνακα βάρους του μοντέλου trainable_weights , τα παράγωγα των μοντέλων βάρη υπολογίζονται από αριστερά προς τα δεξιά, σε όλο το γράφημα υπολογισμού. Δηλαδή, παίρνουμε την τιμή της συνάρτησης απώλειας scaled_loss και βρίσκουμε τα παράγωγα για τις τιμές που λαμβάνονται στην έξοδο της διακόσμησης, στη συνέχεια για τις τιμές που λαμβάνονται στον κωδικοποιητή και ούτω καθεξής μέχρι τις αρχικές τιμές του μοντέλου. Ο στόχος είναι να βρεθεί η αξία των παραγώγων με τέτοιο τρόπο ώστε να ελαχιστοποιηθεί η συνάρτηση απώλειας. Εννοιολογικά, το επιθυμητό πρόγραμμα κατάρτισης νευρωνικών δικτύων μοιάζει με αυτό: η συνάρτηση απώλειας παίρνει μια ελάχιστη τιμή → βρίσκουμε τα βάρη που αντιστοιχούν σε αυτήν την τιμή → Το σφάλμα είναι ελάχιστο → Η πρόβλεψη του νευρικού δικτύου είναι ακριβής. Οπτικά, το σχήμα υπολογισμού διανυσμάτων κλίσης και ο μηχανισμός διάδοσης της πλάτης μπορούν να εμφανιστούν ως εξής. (Εικόνα 11 - Υπολογισμός διανυσματικού διαβάθμισης) (Εικόνα 12 - Μηχανισμός διάδοσης πίσω) ━ loss = all_reduce_sum (απώλεια) ━ sample_size = all_reduce_sum (loss_token_normalizer) ━ Ορμικές και ταχύτητες - αρχικά αρχικά αρχικοποιούνται στο μηδέν. Περιέχουν τις τιμές ορμής για κάθε βάρος του μοντέλου και θα προσαρμοστούν και θα ενημερώνονται με κάθε βήμα. ━ alpha - προσαρμοστική τιμή της παραμέτρου . (Εικόνα 15 - Εφαρμογή διαβαθμίσεων για μοντέλα βάρη) Όταν χρησιμοποιείτε διαφορετικό τύπο βελτιστοποιητή, ο μηχανισμός για τον υπολογισμό και την εφαρμογή των κλίσεων θα είναι διαφορετικός. Απλοποιημένη ακολουθία κλήσεων: ├ .. call () Εκπαιδευτής κλάσης module truct.py ├ .. def _Steps () Trainter <) Trainter <) training.py ├ .. module training.py ├ .. def compute_gradients () Modies () Modies model.py ├ .. module training.py ├ .. def Βελτιστοποιητές/utils.py ├ .. module training.py Μετά την εφαρμογή των κλίσεων, η τιμή της συνάρτησης απώλειας διαιρείται με τον συνολικό αριθμό των μαρκών, απώλεια = float (απώλεια) / float (sample_size) → 40.6409149 / 12 = 3.38674291 . Αυτή είναι η τιμή που θα εμφανιστεί στο αρχείο καταγραφής εκπαίδευσης: βήμα = 1; Απώλεια = 3.386743. Και αυτή η τιμή θα χρησιμοποιηθεί για να σχεδιάσει το γράφημα συνάρτησης απώλειας κατάρτισης που εμφανίζεται στο tensorboard. Το έγγραφο ολοκληρώνεται επισημαίνοντας τις κρίσιμες διαδικασίες που εμπλέκονται στον υπολογισμό της απώλειας και της εφαρμογής των διαβαθμίσεων στα μοντέλα μηχανικής μάθησης. Με την κατανόηση του τρόπου με τον οποίο αλληλεπιδρούν αυτά τα εξαρτήματα, ιδιαίτερα των προσαρμογών για την ευθυγράμμιση και τον προσεκτικό υπολογισμό των κλίσεων, οι ερευνητές μπορούν να βελτιστοποιήσουν καλύτερα τα μοντέλα τους για βελτιωμένη ακρίβεια και απόδοση.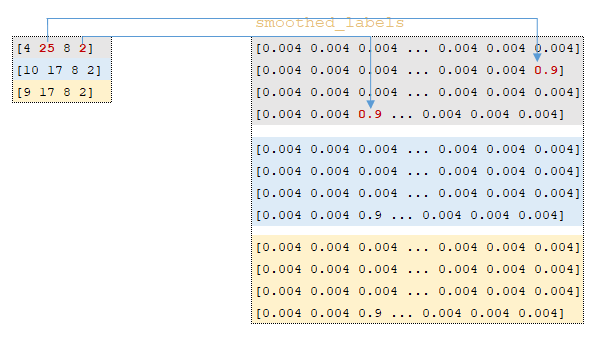


Μηχανισμός ευθυγράμμισης


Μηχανισμός για τον υπολογισμό και την εφαρμογή κλίσεων


Σύναψη
↑